ГДЗ по Геометрии 9 класс Номер 998 Атанасян — Подробные Ответы

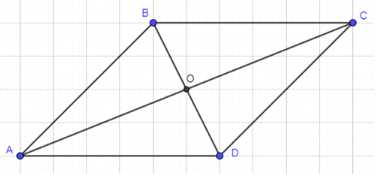
Докажите, что четырёхугольник ABCD, вершины которого имеют координаты A (−2; −3), В (1; 4), C (8; 7), D (5; 0), является ромбом. Найдите его площадь.

Дано: четырехугольник ABCD с координатами A(-2; -3), B(1; 4), C(8; 7), D(5; 0). Нужно доказать, что ABCD — ромб, и найти площадь \( S_{ABCD} \).

1. Найдем длины сторон:

\( AB = \sqrt{(-2 — 1)^2 + (-3 — 4)^2} = \sqrt{58} \)

\( BC = \sqrt{(1 — 8)^2 + (4 — 7)^2} = \sqrt{58} \)

\( CD = \sqrt{(8 — 5)^2 + (7 — 0)^2} = \sqrt{58} \)

\( AD = \sqrt{(-2 — 5)^2 + (-3 — 0)^2} = \sqrt{58} \)

Поскольку AB = BC = CD = AD, то ABCD — ромб.

2. Найдем диагонали:

\( BD = \sqrt{(1 — 5)^2 + (4 — 0)^2} = \sqrt{32} = 4\sqrt{2} \)

\( AC = \sqrt{(-2 — 8)^2 + (-3 — 7)^2} = \sqrt{200} = 10\sqrt{2} \)

3. Площадь ромба:

\( S_{ABCD} = \frac{1}{2} \times AC \times BD = \frac{1}{2} \times 10\sqrt{2} \times 4\sqrt{2} = 20 \times 2 = 40 \, \text{кв. ед.} \)

Ответ: \( S_{ABCD} = 40 \, \text{кв. ед.} \)

Дано: четырехугольник ABCD с координатами A(-2; -3), B(1; 4), C(8; 7), D(5; 0). Требуется доказать, что ABCD — ромб, и найти площадь \( S_{ABCD} \).

1. Вычисление длин сторон:

Для нахождения длины стороны используем формулу расстояния между двумя точками:

\( d = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2} \)

AB:

\( AB = \sqrt{(-2 — 1)^2 + (-3 — 4)^2} = \sqrt{(-3)^2 + (-7)^2} = \sqrt{9 + 49} = \)
\( =\sqrt{58} \approx 7.62 \)

BC:

\( BC = \sqrt{(1 — 8)^2 + (4 — 7)^2} = \sqrt{(-7)^2 + (-3)^2} = \sqrt{49 + 9} = \)
\( =\sqrt{58} \approx 7.62 \)

CD:

\( CD = \sqrt{(8 — 5)^2 + (7 — 0)^2} = \sqrt{3^2 + 7^2} = \sqrt{9 + 49} = \sqrt{58} \approx 7.62 \)

AD:

\( AD = \sqrt{(-2 — 5)^2 + (-3 — 0)^2} = \sqrt{(-7)^2 + (-3)^2} =\sqrt{49 + 9} = \)
\( =\sqrt{58} \approx 7.62 \)

Поскольку AB = BC = CD = AD, то ABCD — ромб.

2. Вычисление диагоналей:

BD:

\( BD = \sqrt{(1 — 5)^2 + (4 — 0)^2} = \sqrt{(-4)^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32} =\)
\( = 4\sqrt{2} \approx 5.66 \)

AC:

\( AC = \sqrt{(-2 — 8)^2 + (-3 — 7)^2} = \sqrt{(-10)^2 + (-10)^2} = \sqrt{100 + 100} = \)
\( =\sqrt{200} = 10\sqrt{2} \approx 14.14 \)

3. Вычисление площади ромба:

Площадь ромба можно найти по формуле через диагонали:

\( S_{ABCD} = \frac{1}{2} \times AC \times BD \)

\( S_{ABCD} = \frac{1}{2} \times 10\sqrt{2} \times 4\sqrt{2} = \frac{1}{2} \times 40 \times 2 = 40 \, \text{кв. ед.} \)

Ответ: \( S_{ABCD} = 40 \, \text{кв. ед.} \)