
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 987 Атанасян — Подробные Ответы
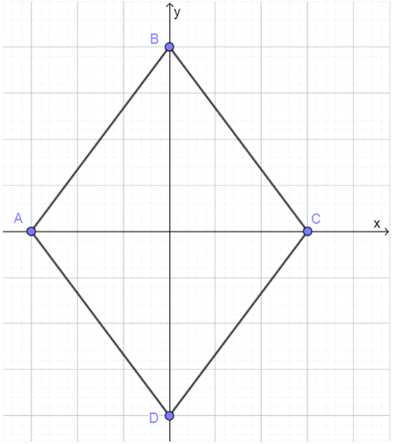
Дан ромб ABCD, диагонали которого равны 2а и 20. Найдите множество всех точек М, для каждой из которых AM² + DM² = BM² + CM².
Дано: ABCD — ромб, AC = 2a, BD = 2b. Найти множество точек М, для которых AM² + DM² = BM² + CM².
Решение:
1) Введем систему координат: AC лежит на оси OX, BD — на оси OY. Координаты точек: A(-a; 0), C(a; 0), B(0; b), D(0; -b). Точка M имеет координаты (x; y).
2) Выразим квадраты расстояний:
AM² = (x + a)² + y²,
DM² = x² + (y + b)²,
BM² = x² + (y — b)²,
CM² = (a — x)² + y².
3) Подставим в условие:
(x + a)² + y² + x² + (y + b)² = x² + (y — b)² + (a — x)² + y².
4) Раскроем скобки и упростим:
x² + 2ax + a² + y² + x² + y² + 2by + b² = x² + y² — 2by + b² + a² — 2ax + x² + y².
5) Сократим подобные члены:
2ax + 2by = -2by — 2ax.
6) Перенесем все члены в одну сторону:
4ax + 4by = 0.
7) Упростим уравнение:
ax + by = 0.
8) Интерпретация результата:
Уравнение ax + by = 0 задает прямую, проходящую через начало координат.
Ответ: Множество всех точек М — это прямая, заданная уравнением ax + by = 0.
Дано: ABCD — ромб, AC = 2a, BD = 2b. Найти множество точек М, для которых AM² + DM² = BM² + CM².
Решение:
1) Введем систему координат:
— Пусть диагональ AC ромба лежит на оси OX, а диагональ BD — на оси OY.
— Координаты вершин ромба: A(-a; 0), C(a; 0), B(0; b), D(0; -b).
— Точка M имеет координаты (x; y).
2) Выразим квадраты расстояний от точки M до вершин ромба:
— AM² = (x + a)² + y² = x² + 2ax + a² + y².
— DM² = x² + (y + b)² = x² + y² + 2by + b².
— BM² = x² + (y — b)² = x² + y² — 2by + b².
— CM² = (a — x)² + y² = a² — 2ax + x² + y².
3) Подставим выражения в условие задачи:
AM² + DM² = BM² + CM²,
(x² + 2ax + a² + y²) + (x² + y² + 2by + b²) = (x² + y² — 2by + b²) + (a² — 2ax + x² + y²).
4) Раскроем скобки и упростим выражение:
x² + 2ax + a² + y² + x² + y² + 2by + b² = x² + y² — 2by + b² + a² — 2ax + x² + y².
5) Сгруппируем подобные члены:
(x² + x²) + (2ax) + (a²) + (y² + y²) + (2by) + (b²) = (x² + x²) + (y² + y²) + (-2by) + (b²) + (a²) + (-2ax).
6) Упростим обе части уравнения:
2x² + 2ax + a² + 2y² + 2by + b² = 2x² + 2y² — 2by + b² + a² — 2ax.
7) Перенесем все члены в левую часть уравнения:
2x² + 2ax + a² + 2y² + 2by + b² — 2x² — 2y² + 2by — b² — a² + 2ax = 0.
8) Сократим подобные члены:
(2x² — 2x²) + (2ax + 2ax) + (a² — a²) + (2y² — 2y²) + (2by + 2by) + (b² — b²) = 0.
9) Получаем:
4ax + 4by = 0.
10) Разделим обе части уравнения на 4:
ax + by = 0.
11) Интерпретация результата:
Уравнение ax + by = 0 задает прямую, проходящую через начало координат.
Ответ: Множество всех точек М — это прямая, заданная уравнением ax + by = 0.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!