
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 977 Атанасян — Подробные Ответы
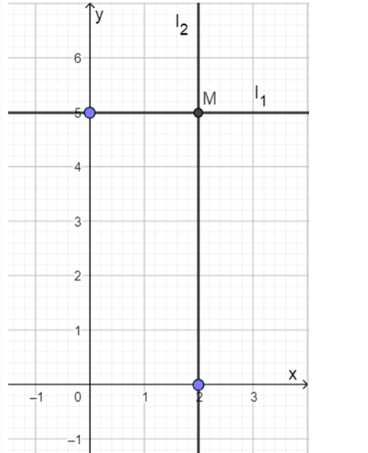
Напишите уравнения прямых, проходящих через точку M (2; 5) и параллельных осям координат.
Дана точка M(2; 5). Найдем уравнения прямых, проходящих через эту точку и параллельных осям координат.
1) Прямая, параллельная оси OX, имеет уравнение вида y = const. Поскольку точка M(2; 5) лежит на этой прямой, её уравнение:
y = 5
2) Прямая, параллельная оси OY, имеет уравнение вида x = const. Поскольку точка M(2; 5) лежит на этой прямой, её уравнение:
x = 2
Ответ: y = 5; x = 2.
Дана точка M(2; 5). Найдем уравнения прямых, проходящих через эту точку и параллельных осям координат.
1) Прямая, параллельная оси OX, имеет уравнение вида y = const. Поскольку точка M(2; 5) лежит на этой прямой, её уравнение:
y = 5
2) Прямая, параллельная оси OY, имеет уравнение вида x = const. Поскольку точка M(2; 5) лежит на этой прямой, её уравнение:
x = 2
Ответ: y = 5; x = 2.
Обоснование:
— Прямая, параллельная оси OX, не изменяет свою координату y, поэтому её уравнение всегда имеет вид y = const.
— Прямая, параллельная оси OY, не изменяет свою координату x, поэтому её уравнение всегда имеет вид x = const.
Таким образом, уравнения прямых, проходящих через точку M(2; 5) и параллельных осям координат, найдены корректно.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!