Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 975 Атанасян — Подробные Ответы
Найдите координаты точек пересечения прямой 3х − 4у + 12 = 0 с осями координат. Начертите эту прямую.
Дано уравнение прямой: 3x − 4y + 12 = 0.
1. Найдем точку пересечения с осью OX (A).
В точке пересечения с осью OX координата y = 0. Подставим y = 0 в уравнение:
3x − 4·0 + 12 = 0
3x + 12 = 0
3x = −12
x = −4
Таким образом, A(−4; 0).
2. Найдем точку пересечения с осью OY (B).
В точке пересечения с осью OY координата x = 0. Подставим x = 0 в уравнение:
3·0 − 4y + 12 = 0
−4y + 12 = 0
−4y = −12
y = 3
Таким образом, B(0; 3).
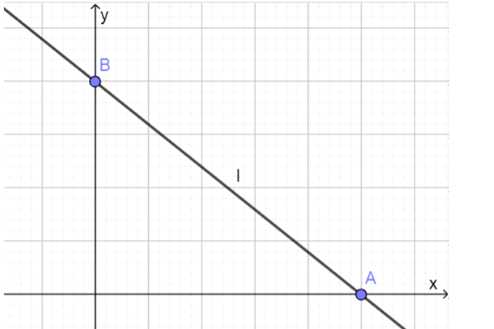
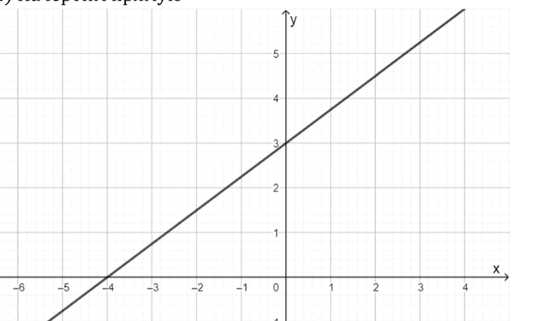
3. Построим прямую по точкам A(−4; 0) и B(0; 3).
Ответ: точки пересечения A(−4; 0) и B(0; 3).
Дано уравнение прямой: 3x − 4y + 12 = 0.
1. Найдем точку пересечения с осью OX (A).
В точке пересечения с осью OX координата y = 0. Подставим y = 0 в уравнение:
3x − 4·0 + 12 = 0
3x + 12 = 0
3x = −12
x = −4
Таким образом, A(−4; 0).
2. Найдем точку пересечения с осью OY (B).
В точке пересечения с осью OY координата x = 0. Подставим x = 0 в уравнение:
3·0 − 4y + 12 = 0
−4y + 12 = 0
−4y = −12
y = 3
Таким образом, B(0; 3).
3. Построим прямую по точкам A(−4; 0) и B(0; 3).
4. Проверим правильность решения:
Подставим координаты точки A(−4; 0) в уравнение прямой:
3·(−4) − 4·0 + 12 = −12 + 0 + 12 = 0.
Подставим координаты точки B(0; 3) в уравнение прямой:
3·0 − 4·3 + 12 = 0 − 12 + 12 = 0.
Оба равенства выполняются, что подтверждает правильность решения.
Ответ: точки пересечения A(−4; 0) и B(0; 3).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.