Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 968 Атанасян — Подробные Ответы
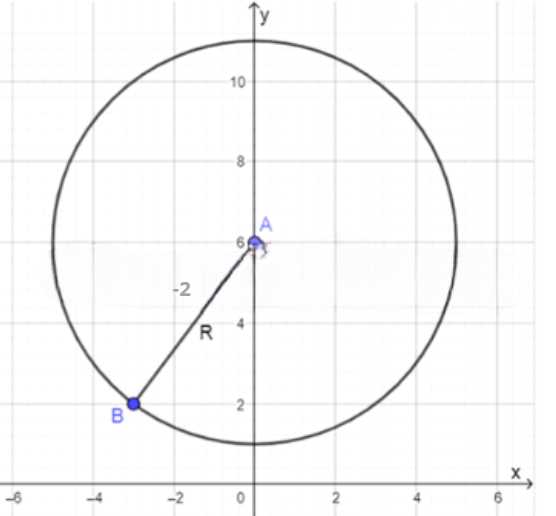
Напишите уравнение окружности с центром в точке А (0; 6), проходящей через точку В (−3; 2).
Дано: окружность с центром в точке \( A(0; 6) \), проходящая через точку \( B(-3; 2) \).
Найдем уравнение окружности.
1. Уравнение окружности с центром в точке \( A(x_0; y_0) \) имеет вид:
\[
(x — x_0)^2 + (y — y_0)^2 = R^2.
\]
Подставляем координаты центра \( A(0; 6) \):
\[
x^2 + (y — 6)^2 = R^2.
\]
2. Найдем радиус \( R \) как расстояние между точками \( A \) и \( B \):
\[
R = \sqrt{(-3 — 0)^2 + (2 — 6)^2} = \sqrt{9 + 16} = \sqrt{25} = 5.
\]
3. Подставляем \( R = 5 \) в уравнение окружности:
\[
x^2 + (y — 6)^2 = 25.
\]
Ответ: уравнение окружности имеет вид \( x^2 + (y — 6)^2 = 25 \).
Дано: окружность с центром в точке \( A(0; 6) \), проходящая через точку \( B(-3; 2) \).
Требуется найти уравнение окружности.
1. Уравнение окружности с центром в точке \( A(x_0; y_0) \) и радиусом \( R \) имеет вид:
\[
(x — x_0)^2 + (y — y_0)^2 = R^2.
\]
Подставляем координаты центра \( A(0; 6) \):
\[
(x — 0)^2 + (y — 6)^2 = R^2,
\]
что упрощается до:
\[
x^2 + (y — 6)^2 = R^2.
\]
2. Найдем радиус \( R \) как расстояние между точками \( A(0; 6) \) и \( B(-3; 2) \). Формула расстояния между двумя точками \( (x_1; y_1) \) и \( (x_2; y_2) \):
\[
R = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}.
\]
Подставляем координаты точек \( A \) и \( B \):
\[
R = \sqrt{(-3 — 0)^2 + (2 — 6)^2} = \sqrt{(-3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5.
\]
3. Подставляем найденное значение радиуса \( R = 5 \) в уравнение окружности:
\[
x^2 + (y — 6)^2 = 5^2,
\]
что упрощается до:
\[
x^2 + (y — 6)^2 = 25.
\]
4. Проверим, что точка \( B(-3; 2) \) лежит на окружности, подставив её координаты в уравнение:
\[
(-3)^2 + (2 — 6)^2 = 9 + 16 = 25.
\]
Левая часть уравнения равна правой, следовательно, точка \( B \) принадлежит окружности.
Ответ: уравнение окружности имеет вид \( x^2 + (y — 6)^2 = 25 \).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.