ГДЗ по Геометрии 9 класс Номер 958 Атанасян — Подробные Ответы

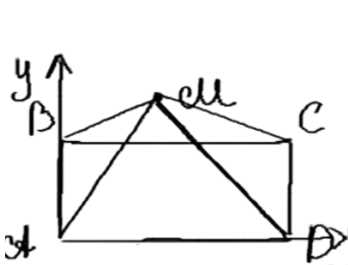
Дан прямоугольник \(ABCD\). Докажите, что для произвольной точки \(M\) плоскости справедливо равенство \(AM^2 + CM^2 = BM^2 + DM^2\).

Для доказательства равенства в прямоугольнике \(ABCD\) для произвольной точки \(M\), введем систему координат:

1. Пусть \(A(0, 0)\), \(B(0, c)\), \(C(a, c)\), \(D(a, 0)\), а точка \(M\) имеет координаты \((x, y)\).

2. Выразим квадраты расстояний:
— \(AM^2 = x^2 + y^2\)
— \(CM^2 = (x-a)^2 + (y-c)^2\)
— \(BM^2 = x^2 + (y-c)^2\)
— \(DM^2 = (x-a)^2 + y^2\)

3. Сложим квадраты расстояний:
— \(AM^2 + CM^2 = x^2 + y^2 + (x-a)^2 + (y-c)^2\)
— \(BM^2 + DM^2 = x^2 + (y-c)^2 + (x-a)^2 + y^2\)

4. Видно, что:
\[
AM^2 + CM^2 = BM^2 + DM^2
\]

Таким образом, равенство доказано.

Дано прямоугольник \(ABCD\), где точки имеют координаты: \(A(0, 0)\), \(B(0, c)\), \(C(a, c)\), \(D(a, 0)\).

Рассмотрим произвольную точку \(M(x, y)\).

1. Найдем квадрат расстояния от точки \(M\) до каждой вершины прямоугольника.

Расстояние \(AM\):
\[
AM = \sqrt{(x — 0)^2 + (y — 0)^2} = \sqrt{x^2 + y^2}
\]
Следовательно, \(AM^2 = x^2 + y^2\).

Расстояние \(CM\):
\[
CM = \sqrt{(x — a)^2 + (y — c)^2}
\]
Следовательно, \(CM^2 = (x — a)^2 + (y — c)^2\).

Расстояние \(BM\):
\[
BM = \sqrt{(x — 0)^2 + (y — c)^2} = \sqrt{x^2 + (y — c)^2}
\]
Следовательно, \(BM^2 = x^2 + (y — c)^2\).

Расстояние \(DM\):
\[
DM = \sqrt{(x — a)^2 + (y — 0)^2} = \sqrt{(x — a)^2 + y^2}
\]
Следовательно, \(DM^2 = (x — a)^2 + y^2\).

2. Теперь сложим квадраты расстояний:

\[
AM^2 + CM^2 = x^2 + y^2 + (x — a)^2 + (y — c)^2
\]

\[
BM^2 + DM^2 = x^2 + (y — c)^2 + (x — a)^2 + y^2
\]

3. Заметим, что обе суммы дают одинаковый результат:

\[
AM^2 + CM^2 = BM^2 + DM^2
\]

Таким образом, для любой точки \(M\) плоскости выполняется равенство \(AM^2 + CM^2 = BM^2 + DM^2\), что и требовалось доказать.