ГДЗ по Геометрии 9 класс Номер 957 Атанасян — Подробные Ответы

Докажите, что если диагонали параллелограмма равны, то параллелограмм является прямоугольником.

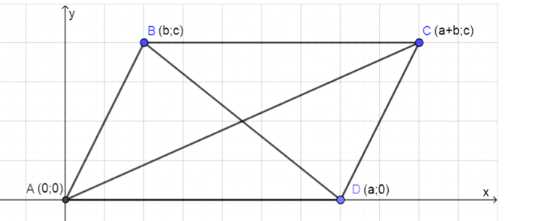
Дано параллелограмм \(ABCD\) с равными диагоналями \(BD = AC\). Нужно доказать, что \(ABCD\) является прямоугольником.

1. Введем прямоугольную систему координат:
— \(A(0, 0)\)
— \(B(b, c)\)
— \(C(a+b, c)\)
— \(D(a, 0)\)

2. По условию \(BD = AC\), следовательно, \((a-b)^2 + c^2 = (a+b)^2 + c^2\).

3. Упростим уравнение:
\(
(a-b)^2 = (a+b)^2
\)
\(
a^2 — 2ab + b^2 = a^2 + 2ab + b^2
\)
\(
-4ab = 0
\)

4. Из этого следует, что \(ab = 0\). Поскольку \(a \neq 0\), то \(b = 0\).

5. Таким образом, точка \(B(0, c)\) лежит на оси \(OY\), и угол \(\angle BAD = 90^\circ\).

Следовательно, параллелограмм \(ABCD\) является прямоугольником, что и требовалось доказать.

Рассмотрим параллелограмм \(ABCD\) с равными диагоналями \(BD = AC\). Нужно доказать, что \(ABCD\) является прямоугольником.

1. Введем прямоугольную систему координат, где:

— \(A(0, 0)\)
— \(B(b, c)\)
— \(C(a+b, c)\)
— \(D(a, 0)\)

2. Выразим длины диагоналей.
Диагональ \(BD\) имеет длину:
\(
BD = \sqrt{(a-b)^2 + (0-c)^2} = \sqrt{(a-b)^2 + c^2}
\)

Диагональ \(AC\) имеет длину:
\(
AC = \sqrt{(a+b-0)^2 + (c-0)^2} = \sqrt{(a+b)^2 + c^2}
\)

3. По условию \(BD = AC\), следовательно, \((a-b)^2 + c^2 = (a+b)^2 + c^2\).

4. Упростим уравнение:
\(
(a-b)^2 = (a+b)^2
\)

Раскроем скобки:
\(
a^2 — 2ab + b^2 = a^2 + 2ab + b^2
\)

Упростим:
\(
-4ab = 0
\)

5. Решим уравнение \(-4ab = 0\). Поскольку \(a \neq 0\), то \(b = 0\).

6. Таким образом, точка \(B(0, c)\) лежит на оси \(OY\), и угол \(\angle BAD = 90^\circ\).

Следовательно, параллелограмм \(ABCD\) является прямоугольником, что и требовалось доказать.