ГДЗ по Геометрии 9 класс Номер 956 Атанасян — Подробные Ответы

Докажите, что в равнобедренной трапеции диагонали равны. Сформулируйте и докажите обратное утверждение.

Для доказательства, что в равнобедренной трапеции диагонали равны, и обратного утверждения, используем координатный метод.

1. Доказательство равенства диагоналей в равнобедренной трапеции:

Пусть \(ABCD\) — равнобедренная трапеция с основаниями \(AD\) и \(BC\). Введем прямоугольную систему координат:
— \(A(-a, 0)\), \(D(a, 0)\)
— \(B(-b, h)\), \(C(b, h)\)

Вычислим длины диагоналей:
\[
BD = \sqrt{(a + b)^2 + h^2}
\]
\[
AC = \sqrt{(b + a)^2 + h^2}
\]

Поскольку \(BD = AC\), диагонали равны, что и требовалось доказать.

2. Обратное утверждение: если диагонали равны, то трапеция равнобедренная:

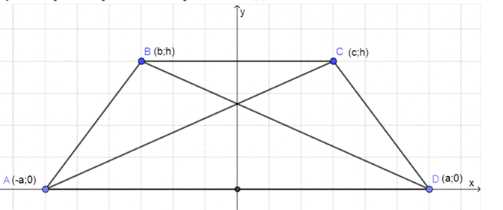
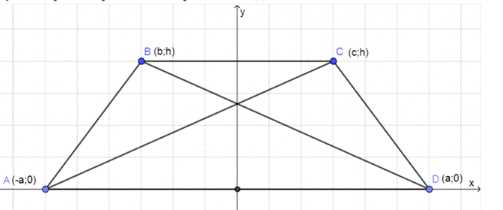
Пусть \(\triangle ABCD\) — трапеция, где \(AC = BD\). Используем координаты:
— \(A(-a, 0)\), \(D(a, 0)\)
— \(B(b, h)\), \(C(c, h)\)

Из условия равенства диагоналей:
\[
AC^2 = (c + a)^2 + h^2
\]
\[
BD^2 = (a — b)^2 + h^2
\]

Если \((c + a)^2 + h^2 = (a — b)^2 + h^2\), то
\[
(c + a)^2 = (a — b)^2
\]

Решая уравнение, получаем:
\[
c + a = a — b \quad \text{или} \quad c + a = b — a
\]

В обоих случаях \(c = -b\). Это значит, что точки \(B\) и \(C\) симметричны относительно оси \(OY\), следовательно, трапеция равнобедренная.

Таким образом, доказано, что равенство диагоналей в трапеции влечет её равнобедренность.

Для доказательства утверждений используем координатный метод.

1. Доказательство равенства диагоналей в равнобедренной трапеции:

Рассмотрим равнобедренную трапецию \(ABCD\) с основаниями \(AD\) и \(BC\). Введем прямоугольную систему координат, где ось \(OY\) является осью симметрии трапеции:
— \(A(-a, 0)\), \(D(a, 0)\)
— \(B(-b, h)\), \(C(b, h)\)

Вычислим длины диагоналей \(BD\) и \(AC\).

Для диагонали \(BD\):
\[
BD = \sqrt{(a + b)^2 + (0 — h)^2} = \sqrt{(a + b)^2 + h^2}
\]

Для диагонали \(AC\):
\[
AC = \sqrt{(b + a)^2 + (h — 0)^2} = \sqrt{(a + b)^2 + h^2}
\]

Поскольку \(BD = AC\), диагонали равны, что и требовалось доказать.

2. Обратное утверждение: если диагонали равны, то трапеция равнобедренная:

Пусть трапеция \(ABCD\) такая, что \(AC = BD\). Введем координаты:
— \(A(-a, 0)\), \(D(a, 0)\)
— \(B(b, h)\), \(C(c, h)\)

Из условия равенства диагоналей:
\[
AC^2 = (c + a)^2 + h^2
\]
\[
BD^2 = (a — b)^2 + h^2
\]

Приравняем выражения:
\[
(c + a)^2 + h^2 = (a — b)^2 + h^2
\]

Упростим:
\[
(c + a)^2 = (a — b)^2
\]

Решим уравнение:
\[
c + a = a — b \quad \text{или} \quad c + a = b — a
\]

Первый случай приводит к \(c = -b\), второй — к \(c = -b\). В обоих случаях точки \(B\) и \(C\) симметричны относительно оси \(OY\), следовательно, трапеция равнобедренная.

Таким образом, доказано, что равенство диагоналей в трапеции влечет её равнобедренность.