ГДЗ по Геометрии 9 класс Номер 952 Атанасян — Подробные Ответы

Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.
Решение
Рассмотрим прямоугольный треугольник АВС с прямым углом С. Обозначим буквой М середину гипотенузы АВ.

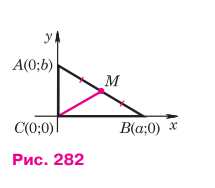
Введём прямоугольную систему координат так, как показано на рисунке 282.

Если BC= a, AC=b, то вершины треугольника имеют координаты С (0; 0), В (а; 0), А (0; b). По формулам координат середины отрезка находим координаты точки М:
\[ M \left( \frac{a}{2}; \frac{b}{2} \right) \].

Пользуясь формулой расстояния между двумя точками, найдём длины отрезков МС и МА:
\[ MC = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2} = \frac{1}{2} \sqrt{a^2 + b^2} \],

\[ MA = \sqrt{\left(\frac{a}{2} — a\right)^2 + \left(\frac{b}{2} — b\right)^2} = \frac{1}{2} \sqrt{a^2 + b^2} \].

Таким образом, \( MA = MB = MC \), что и требовалось доказать.

Для доказательства того, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин, используем координатный метод.

1. Введем систему координат:
— \( C(0, 0) \), \( B(a, 0) \), \( A(0, b) \).

2. Найдем координаты середины гипотенузы \( AB \):
— \( M \left( \frac{a}{2}, \frac{b}{2} \right) \).

3. Рассчитаем расстояния от точки \( M \) до вершин \( C \) и \( A \):

— \( MC = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2} = \frac{1}{2} \sqrt{a^2 + b^2} \).

— \( MA = \sqrt{\left(\frac{a}{2} — a\right)^2 + \left(\frac{b}{2} — b

Рассмотрим прямоугольный треугольник \(ABC\) с прямым углом в точке \(C\). Пусть \(BC = a\) и \(AC = b\).

Нам нужно доказать, что середина гипотенузы \(AB\) равноудалена от всех вершин треугольника.

1. Введем систему координат:
— Точка \(C\) имеет координаты \((0, 0)\).
— Точка \(B\) имеет координаты \((a, 0)\).
— Точка \(A\) имеет координаты \((0, b)\).

2. Найдем координаты середины гипотенузы \(AB\), обозначим эту точку как \(M\). Координаты точки \(M\) вычисляются по формуле для середины отрезка:
— \(M\left(\frac{a}{2}, \frac{b}{2}\right)\).

3. Вычислим расстояние от точки \(M\) до точки \(C\):
— \(MC = \sqrt{\left(\frac{a}{2} — 0\right)^2 + \left(\frac{b}{2} — 0\right)^2} = \sqrt{\frac{a^2}{4} + \frac{b^2}{4}} = \sqrt{\frac{a^2 + b^2}{4}} = \frac{\sqrt{a^2 + b^2}}{2}\).

4. Вычислим расстояние от точки \(M\) до точки \(A\):
— \(MA = \sqrt{\left(0 — \frac{a}{2}\right)^2 + \left(b — \frac{b}{2}\right)^2} = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2} = \sqrt{\frac{a^2}{4} + \frac{b^2}{4}} = \frac{\sqrt{a^2 + b^2}}{2}\).

5. Вычислим расстояние от точки \(M\) до точки \(B\):
— \(MB = \sqrt{\left(a — \frac{a}{2}\right)^2 + \left(0 — \frac{b}{2}\right)^2} = \sqrt{\left(\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2} = \sqrt{\frac{a^2}{4} + \frac{b^2}{4}} = \frac{\sqrt{a^2 + b^2}}{2}\).

Таким образом, мы доказали, что \(MC = MA = MB = \frac{\sqrt{a^2 + b^2}}{2}\). Это означает, что середина гипотенузы \(AB\) равноудалена от всех вершин треугольника \(ABC\).