ГДЗ по Геометрии 9 класс Номер 933 Атанасян — Подробные Ответы

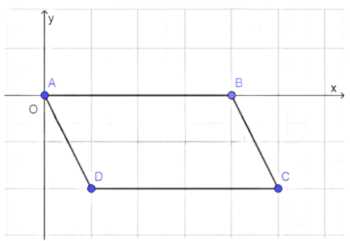
Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), В (5; 0), С (12; -3.).

Чтобы найти координаты вершины \( D \) параллелограмма \( ABCD \), используем правило, что в параллелограмме диагонали делятся пополам.

Для нахождения координат \( D \) используем векторное уравнение:

\[
\vec{AD} = \vec{AC} — \vec{AB}
\]

Координаты точек:
— \( A(0, 0) \)
— \( B(5, 0) \)
— \( C(12, -3) \)

Вычисляем координаты \( D \):

1. \[ x_D = x_C — x_B = 12 — 5 = 7 \]
2. \[ y_D = y_C — y_B = -3 — 0 = -3 \]

Таким образом, координаты точки \( D \) равны \( (7, -3) \).

Для нахождения координат вершины \( D \) параллелограмма \( ABCD \), где известны координаты \( A(0, 0) \), \( B(5, 0) \), и \( C(12, -3) \), используем следующее правило: в параллелограмме диагонали делятся пополам.

Рассмотрим векторное уравнение:

\[
\vec{AD} = \vec{AC} — \vec{AB}
\]

1. Найдем вектор \(\vec{AC}\):
— \( x_C — x_A = 12 — 0 = 12 \)
— \( y_C — y_A = -3 — 0 = -3 \)
— Таким образом, \(\vec{AC} = (12, -3)\)

2. Найдем вектор \(\vec{AB}\):
— \( x_B — x_A = 5 — 0 = 5 \)
— \( y_B — y_A = 0 — 0 = 0 \)
— Таким образом, \(\vec{AB} = (5, 0)\)

3. Используя уравнение \(\vec{AD} = \vec{AC} — \vec{AB}\), получаем:
— \( x_D = x_C — x_B = 12 — 5 = 7 \)
— \( y_D = y_C — y_B = -3 — 0 = -3 \)

Таким образом, координаты точки \( D \) равны \( (7, -3) \).

Это решение показывает, как использовать свойства параллелограмма и векторные уравнения для нахождения неизвестной вершины.