ГДЗ по Геометрии 9 класс Номер 932 Атанасян — Подробные Ответы

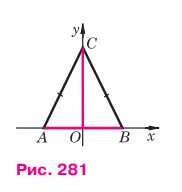
Найдите координаты вершин равнобедренного треугольника АВС, изображённого на рисунке 281, если АВ=2а, а высота СО равна h.

Для нахождения координат вершин равнобедренного треугольника \( \triangle ABC \) с основанием \( AB = 2a \) и высотой \( CO = h \), следуем следующим шагам:

1. Поскольку \( CO \) является высотой и медианой, точка \( O \) делит \( AB \) пополам. Следовательно, \( AO = OB = a \).

2. Координаты вершины \( A \) будут \((-a, 0)\), так как она находится на оси \( x \) слева от центра.

3. Координаты вершины \( B \) будут \((a, 0)\), так как она находится на оси \( x \) справа от центра.

4. Координаты вершины \( C \) будут \((0, h)\), так как она лежит на высоте \( h \) над центром.

Таким образом, координаты вершин треугольника \( \triangle ABC \) следующие:
— \( A(-a, 0) \)
— \( B(a, 0) \)
— \( C(0, h) \)

Рассмотрим равнобедренный треугольник \( \triangle ABC \), где основание \( AB = 2a \) и высота \( CO = h \).

1. Поскольку треугольник равнобедренный, высота \( CO \) является также медианой. Это значит, что точка \( O \) — середина отрезка \( AB \).

2. Найдем координаты точек \( A \) и \( B \). Поскольку \( AB = 2a \), то:
— \( AO = OB = \frac{AB}{2} = a \).

3. Введем систему координат, где точка \( O \) находится в начале координат (0,0). Тогда:
— \( A \) будет находиться слева от \( O \) на расстоянии \( a \): \( A(-a, 0) \).
— \( B \) будет находиться справа от \( O \) на расстоянии \( a \): \( B(a, 0) \).

4. Высота \( CO = h \) будет проходить через точку \( O \) и пересекать линию \( AB \) перпендикулярно. Вершина \( C \) будет находиться на высоте \( h \) над точкой \( O \): \( C(0, h) \).

Таким образом, координаты вершин треугольника \( \triangle ABC \) будут следующими:
— \( A(-a, 0) \)
— \( B(a, 0) \)
— \( C(0, h) \)

Это решение учитывает, что треугольник равнобедренный и высота является медианой, что позволяет легко определить координаты всех вершин.