ГДЗ по Геометрии 9 класс Номер 931 Атанасян — Подробные Ответы

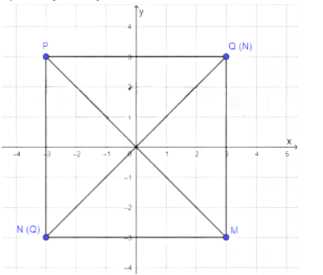
Начертите квадрат \(MNPQ\) так, чтобы вершина \(P\) имела координаты \((-3; 3)\), а диагонали квадрата пересекались в начале координат. Найдите координаты точек \(M\), \(N\) и \(Q\).

Для решения задачи нам нужно определить координаты вершин квадрата \(MNPQ\), зная, что диагонали пересекаются в начале координат и точка \(P\) имеет координаты \((-3, 3)\).

Диагонали квадрата делят друг друга пополам, поэтому центр квадрата находится в начале координат \((0, 0)\). Это значит, что если одна вершина квадрата имеет координаты \((-3, 3)\), то противоположная вершина будет иметь координаты \((3, -3)\).

Теперь найдем оставшиеся две вершины:

1. Вершина \(Q\) или \(N\) будет находиться на горизонтальной линии, проходящей через центр, и иметь координаты \((3, 3)\).
2. Вершина \(N\) или \(Q\) будет находиться на вертикальной линии, проходящей через центр, и иметь координаты \((-3, -3)\).

Таким образом, возможны два решения в зависимости от обозначения:

1. \(P(-3, 3)\), \(Q(3, 3)\), \(M(3, -3)\), \(N(-3, -3)\)
2. \(P(-3, 3)\), \(Q(-3, -3)\), \(M(3, -3)\), \(N(3, 3)\)

Задача имеет два решения, так как квадрат можно повернуть на 90 градусов вокруг начала координат.

Для решения задачи начнем с анализа условий. У нас есть квадрат MNPQ с вершиной P(-3, 3), и диагонали квадрата пересекаются в начале координат (0, 0).

1. Центр квадрата: Диагонали квадрата пересекаются в центре, который совпадает с началом координат (0, 0).

2. Координаты противоположной вершины: Если одна вершина квадрата P имеет координаты (-3, 3), то противоположная вершина M будет иметь координаты (3, -3). Это связано с тем, что центр квадрата является серединой диагонали, и координаты противоположных вершин симметричны относительно центра.

3. Координаты оставшихся вершин:
— Вершина Q будет находиться на горизонтальной линии, проходящей через центр, и иметь ту же ординату, что и P, но противоположную абсциссу, то есть (3, 3).
— Вершина N будет находиться на вертикальной линии, проходящей через центр, и иметь ту же абсциссу, что и P, но противоположную ординату, то есть (-3, -3).

Таким образом, мы нашли координаты всех вершин квадрата:

1. P(-3, 3)
2. Q(3, 3)
3. M(3, -3)
4. N(-3, -3)

Однако, так как квадрат можно повернуть на 90 градусов вокруг центра, возможна перестановка вершин:

1. P(-3, 3)
2. Q(-3, -3)
3. M(3, -3)
4. N(3, 3)

Таким образом, задача имеет два решения в зависимости от обозначения вершин квадрата.