ГДЗ по Геометрии 9 класс Номер 918 Атанасян — Подробные Ответы

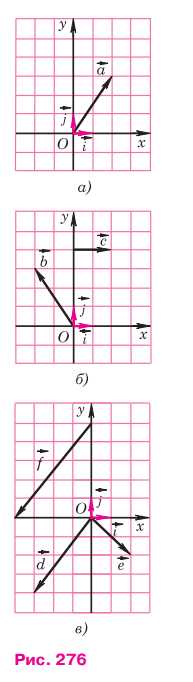
918 Разложите векторы \(\vec{a}\), \(\vec{b}\), \(\vec{c}\), \(\vec{d}\), \(\vec{e}\) и \(\vec{j}\), изображённые на рисунке 276, \(\vec{a}\), \(\vec{b}\), \(\vec{v}\), по координатным векторам \(\vec{i}\) и \(\vec{j}\) и найдите их координаты.

Для разложения векторов по координатным векторам \(\vec{i}\) и \(\vec{j}\), нужно определить их координаты:

1. \(\vec{a} = 2\vec{i} + 3\vec{j}\) \(\Rightarrow\) \(\vec{a} \{2; 3\}\)
2. \(\vec{b} = -2\vec{i} + 3\vec{j}\) \(\Rightarrow\) \(\vec{b} \{-2; 3\}\)
3. \(\vec{c} = 2\vec{i}\) \(\Rightarrow\) \(\vec{c} \{2; 0\}\)
4. \(\vec{d} = -3\vec{i} — 4\vec{j}\) \(\Rightarrow\) \(\vec{d} \{-3; -4\}\)
5. \(\vec{e} = 2\vec{i} — 2\vec{j}\) \(\Rightarrow\) \(\vec{e} \{2; -2\}\)
6. \(\vec{f} = -4\vec{i} — 5\vec{j}\) \(\Rightarrow\) \(\vec{f} \{-4; -5\}\)

Таким образом, координаты всех векторов выражены через базисные векторы \(\vec{i}\) и \(\vec{j}\).

Для разложения векторов \(\vec{a}\), \(\vec{b}\), \(\vec{c}\), \(\vec{d}\), \(\vec{e}\) и \(\vec{f}\), изображённых на рисунке, по координатным векторам \(\vec{i}\) и \(\vec{j}\), выполним следующие шаги:

1. Вектор \(\vec{a}\) направлен вправо и вверх. Он проходит 2 единичных отрезка по оси \(x\) и 3 единичных отрезка по оси \(y\).
Таким образом, \(\vec{a} = 2\vec{i} + 3\vec{j}\), и его координаты: \(\{2; 3\}\).

2. Вектор \(\vec{b}\) направлен влево и вверх. Он проходит 2 единичных отрезка влево по оси \(x\) и 3 единичных отрезка вверх по оси \(y\).
Таким образом, \(\vec{b} = -2\vec{i} + 3\vec{j}\), и его координаты: \(\{-2; 3\}\).

3. Вектор \(\vec{c}\) направлен вправо вдоль оси \(x\). Он проходит 2 единичных отрезка по оси \(x\) и не поднимается по оси \(y\).
Таким образом, \(\vec{c} = 2\vec{i}\), и его координаты: \(\{2; 0\}\).

4. Вектор \(\vec{d}\) направлен влево и вниз. Он проходит 3 единичных отрезка влево по оси \(x\) и 4 единичных отрезка вниз по оси \(y\).
Таким образом, \(\vec{d} = -3\vec{i} — 4\vec{j}\), и его координаты: \(\{-3; -4\}\).

5. Вектор \(\vec{e}\) направлен вправо и вниз. Он проходит 2 единичных отрезка вправо по оси \(x\) и 2 единичных отрезка вниз по оси \(y\).
Таким образом, \(\vec{e} = 2\vec{i} — 2\vec{j}\), и его координаты: \(\{2; -2\}\).

6. Вектор \(\vec{f}\) направлен влево и вниз. Он проходит 4 единичных отрезка влево по оси \(x\) и 5 единичных отрезков вниз по оси \(y\).
Таким образом, \(\vec{f} = -4\vec{i} — 5\vec{j}\), и его координаты: \(\{-4; -5\}\).

Таким образом, все векторы успешно разложены по базисным векторам \(\vec{i}\) и \(\vec{j}\), и их координаты определены.