
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 912 Атанасян — Подробные Ответы
Конечно, вот извлечённый текст:
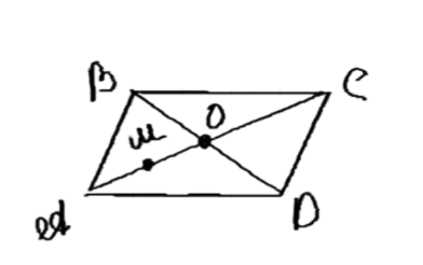
Диагонали параллелограмма ABCD пересекаются в точке O, M — середина отрезка AO. Найдите, если это возможно, такое число k, чтобы выполнялось равенство:
а) \(\overrightarrow{AC} = k\overrightarrow{AO}\);
б) \(\overrightarrow{BO} = k\overrightarrow{BD}\);
в) \(\overrightarrow{OC} = k\overrightarrow{CA}\);
г) \(\overrightarrow{AB} = k\overrightarrow{DC}\);
д) \(\overrightarrow{BC} = k\overrightarrow{DA}\);
е) \(\overrightarrow{AM} = k\overrightarrow{CA}\);
ж) \(\overrightarrow{MC} = k\overrightarrow{AM}\);
з) \(\overrightarrow{AC} = k\overrightarrow{CM}\);
и) \(\overrightarrow{AO} = k\overrightarrow{BD}\).
Давайте рассмотрим решение задачи.
а) \(\overrightarrow{AC} = k\overrightarrow{AO}\); \(\overrightarrow{AC} \uparrow\uparrow \overrightarrow{AO}\)
\(k > 0 \Rightarrow |\overrightarrow{AC}| = 2|\overrightarrow{AO}| \Rightarrow k = 2\)
б) \(\overrightarrow{BO} = k\overrightarrow{BD}\); \(\overrightarrow{BO} \uparrow\uparrow \overrightarrow{BD}\)
\(k > 0 \Rightarrow |\overrightarrow{BO}| = \frac{1}{2}|\overrightarrow{BD}| \Rightarrow k = \frac{1}{2}\)
в) \(\overrightarrow{OC} = k\overrightarrow{CA}\); \(\overrightarrow{OC} \downarrow \overrightarrow{CA}\)
\(k < 0 \Rightarrow |\overrightarrow{OC}| = \frac{1}{2}|\overrightarrow{CA}| \Rightarrow k = -\frac{1}{2}\)
г) \(\overrightarrow{AB} = k\overrightarrow{DC}\); \(\overrightarrow{AB} \uparrow\uparrow \overrightarrow{DC}\)
\(k > 0 \Rightarrow |\overrightarrow{AB}| = |\overrightarrow{DC}| \Rightarrow k = 1\)
д) \(\overrightarrow{BC} = k\overrightarrow{DA}\); \(\overrightarrow{BC} \downarrow \overrightarrow{DA}\)
\(k < 0 \Rightarrow |\overrightarrow{BC}| = |\overrightarrow{DA}| \Rightarrow k = -1\)
е) \(\overrightarrow{AM} = k\overrightarrow{CA}\); \(\overrightarrow{AM} \downarrow \overrightarrow{CA}\)
\(k < 0 \Rightarrow |\overrightarrow{AM}| = \frac{1}{4}|\overrightarrow{CA}| \Rightarrow k = -\frac{1}{4}\)
ж) \(\overrightarrow{MC} = k\overrightarrow{AM}\); \(\overrightarrow{MC} \uparrow\uparrow \overrightarrow{AM}\)
\(k > 0 \Rightarrow |\overrightarrow{MC}| = 3|\overrightarrow{AM}| \Rightarrow k = 3\)
з) \(\overrightarrow{AC} = k\overrightarrow{CM}\); \(\overrightarrow{AC} \downarrow \overrightarrow{CM}\)
\(k < 0 \Rightarrow |\overrightarrow{AC}| = \frac{4}{3}|\overrightarrow{CM}| \Rightarrow k = -\frac{4}{3}\)
и) \(\overrightarrow{AO} = k\overrightarrow{BD}\);
\(\overrightarrow{AO}\) и \(\overrightarrow{BD}\) — неколлинеарны, следовательно их нельзя разложить.
Давайте подробно разберем каждую часть задачи.
а) Рассмотрим вектор \(\overrightarrow{AC}\) и \(\overrightarrow{AO}\). Так как диагонали параллелограмма пересекаются в точке O и делятся пополам, то \(\overrightarrow{AC} = 2\overrightarrow{AO}\). Это означает, что \(k = 2\).
б) Для векторов \(\overrightarrow{BO}\) и \(\overrightarrow{BD}\), так как O — середина диагонали \(\overrightarrow{BD}\), получаем \(\overrightarrow{BO} = \frac{1}{2}\overrightarrow{BD}\). Следовательно, \(k = 0,5\).
в) Векторы \(\overrightarrow{OC}\) и \(\overrightarrow{CA}\) имеют противоположное направление, и \(|\overrightarrow{OC}| = \frac{1}{2}|\overrightarrow{CA}|\). Это дает \(k = -0,5\).
г) Векторы \(\overrightarrow{AB}\) и \(\overrightarrow{DC}\) равны по длине и направлению, так как они противоположные стороны параллелограмма. Следовательно, \(k = 1\).
д) Векторы \(\overrightarrow{BC}\) и \(\overrightarrow{DA}\) равны по длине, но противоположны по направлению, так как они также противоположные стороны параллелограмма. Это дает \(k = -1\).
е) Для векторов \(\overrightarrow{AM}\) и \(\overrightarrow{CA}\), \(|\overrightarrow{AM}| = \frac{1}{4}|\overrightarrow{CA}|\) и направления противоположны, следовательно, \(k = -0,25\).
ж) Векторы \(\overrightarrow{MC}\) и \(\overrightarrow{AM}\) имеют одно направление, и \(|\overrightarrow{MC}| = 3|\overrightarrow{AM}|\). Это дает \(k = 3\).
з) Векторы \(\overrightarrow{AC}\) и \(\overrightarrow{CM}\) имеют противоположное направление, и \(|\overrightarrow{AC}| = \frac{4}{3}|\overrightarrow{CM}|\). Следовательно, \(k = -\frac{4}{3}\).
и) Для векторов \(\overrightarrow{AO}\) и \(\overrightarrow{BD}\), так как они неколлинеарны, разложить их невозможно, и \(k\) не существует.
Таким образом, мы получили значения \(k\) для всех возможных случаев.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!