ГДЗ по Геометрии 9 класс Номер 910 Атанасян — Подробные Ответы

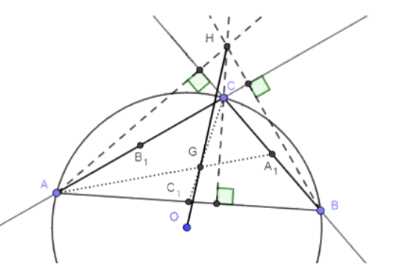
Пусть H — точка пересечения прямых, содержащих высоты неравностороннего треугольника ABC, а O — центр описанной около этого треугольника окружности. Используя векторы, докажите, что точка G пересечения медиан треугольника принадлежит отрезку HO и делит этот отрезок в отношении 2 : 1, считая от точки H, т. е.

\[
\frac{HG}{GO} = 2
\]

Дано: \( \triangle ABC \), \( A_1, B_1, C_1 \) — середины сторон; \( H \) — точка пересечения высот; \( G \) — точка пересечения медиан. Требуется доказать, что \( G \in OH \) и \( \frac{HG}{GO} = 2 \).

**Доказательство:**

1. По правилу треугольника:
\[
\vec{A_1O} + \vec{OG} = \vec{A_1G}, \quad \vec{AH} + \vec{HG} = \vec{AG}.
\]

2. По теореме о пересечении медиан:
\[
\vec{AG} = -2 \vec{A_1G}.
\]
Подставляя это в вышеуказанное равенство:
\[
\vec{AH} + \vec{HG} = -2 \vec{A_1O} — 2 \vec{OG}.
\]

3. Векторы \( \vec{AH} \) и \( \vec{A_1O} \) коллинеарны, значит, существует число \( x \), такое что:
\[
\vec{A_1O} = x \vec{AH}.
\]

4. Тогда:
\[
\vec{HG} + 2 \vec{OG} = -(2x + 1) \vec{AH}.
\]

5. Аналогично для другой стороны:
\[
\vec{HG} + 2 \vec{OG} = -(2m + 1) \vec{BH},
\]
где \( m \) определяется из равенства:
\[
\vec{B_1O} = m \vec{BH}.
\]

6. Так как \( \vec{AH} \) и \( \vec{BH} \) не коллинеарны, то:
\[
\vec{HG} + 2 \vec{OG} = 0.
\]
Отсюда:
\[
\vec{HG} = -2 \vec{OG}.
\]

7. Это означает, что точка \( G \) принадлежит отрезку \( OH \), и:
\[
\frac{HG}{GO} = 2.
\]
Что и требовалось доказать.

Дано: \( \triangle ABC \), \( A_1, B_1, C_1 \) — середины сторон треугольника; \( H \) — точка пересечения высот (ортоцентр); \( G \) — точка пересечения медиан (центроид). Требуется доказать, что \( G \in OH \) и \( \frac{HG}{GO} = 2 \).

Решение:

1. Рассмотрим правило сложения векторов для треугольника. Для любой точки на медиане выполняются равенства:
\[
\vec{A_1O} + \vec{OG} = \vec{A_1G}, \quad \vec{AH} + \vec{HG} = \vec{AG}.
\]
Это следует из свойств медиан и высот треугольника.

2. По теореме о пересечении медиан известно, что точка \( G \) делит медиану в отношении \( 2:1 \), считая от вершины треугольника. Следовательно:
\[
\vec{AG} = -2 \vec{A_1G}.
\]
Подставляя это в формулу для \( \vec{AG} \), получаем:
\[
\vec{AH} + \vec{HG} = -2 \vec{A_1O} — 2 \vec{OG}.
\]

3. Векторы \( \vec{AH} \) и \( \vec{A_1O} \) коллинеарны, поскольку точка \( A_1 \) лежит на медиане, соединяющей вершину \( A \) с серединой противоположной стороны. Значит, существует число \( x \), такое что:
\[
\vec{A_1O} = x \vec{AH}.
\]

4. Подставляя \( \vec{A_1O} = x \vec{AH} \) в равенство, получаем:
\[
\vec{HG} + 2 \vec{OG} = -(2x + 1) \vec{AH}.
\]

5. Аналогично для другой медианы \( \vec{BH} \), соединяющей вершину \( B \) с серединой противоположной стороны \( B_1 \), выполняется равенство:
\[
\vec{HG} + 2 \vec{OG} = -(2m + 1) \vec{BH},
\]
где \( m \) определяется из равенства:
\[
\vec{B_1O} = m \vec{BH}.
\]

6. Поскольку векторы \( \vec{AH} \) и \( \vec{BH} \) не коллинеарны (они направлены вдоль разных высот треугольника), то из равенства:
\[
\vec{HG} + 2 \vec{OG} = 0,
\]
следует, что:
\[
\vec{HG} = -2 \vec{OG}.
\]

7. Таким образом, точка \( G \) принадлежит прямой \( OH \), и отношение длин векторов \( \vec{HG} \) и \( \vec{GO} \) равно:
\[
\frac{HG}{GO} = 2.
\]

Ответ: точка \( G \) лежит на прямой \( OH \) и делит её в отношении \( 2:1 \), считая от точки \( H \).