ГДЗ по Геометрии 9 класс Номер 909 Атанасян — Подробные Ответы

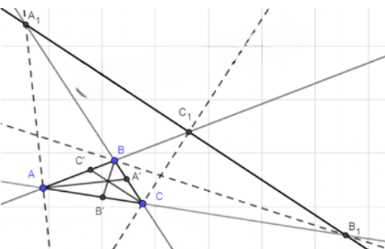
Биссектрисы внешних углов треугольника \( ABC \) при вершинах \( A, B \) и \( C \) пересекают прямые \( BC, CA \) и \( AB \) соответственно в точках \( A_1, B_1 \) и \( C_1 \). Используя векторы, докажите, что точки \( A_1, B_1 \) и \( C_1 \) лежат на одной прямой. 

Дано: треугольник \( \triangle ABC \), \( AA_1, BB_1, CC_1 \) — биссектрисы внешних углов. \( AA_1 \cap BC = A_1 \), \( BB_1 \cap AC = B_1 \), \( CC_1 \cap AB = C_1 \). Требуется доказать, что точки \( A_1, B_1, C_1 \) лежат на одной прямой.

Решение:

1. Пусть \( BC = a \), \( AC = b \), \( AB = c \).

2. Направим единичные векторы вдоль сторон треугольника:
\[
\vec{CB} = a \vec{i}, \quad \vec{CA} = b \vec{j}, \quad \vec{BA} = c \vec{k}.
\]

3. Согласно теореме о биссектрисе внешнего угла:
\[
\frac{CA_1}{A_1B} = \frac{AC}{AB} > 1.
\]
Следовательно:
\[
\frac{CA_1}{CA_1 — BC} = \frac{AB}{AC}.
\]
Упрощаем:
\[
CA_1 = \frac{ab}{b — c}.
\]
Тогда:
\[
\vec{CA_1} = \frac{ab}{b — c} \vec{i}.
\]

4. Аналогично для \( B_1 \):
\[
\frac{CB_1}{B_1A} = \frac{BC}{AB} > 1.
\]
Следовательно:
\[
CB_1 = \frac{ac}{a — c}.
\]
Тогда:
\[
\vec{CB_1} = \frac{ac}{a — c} \vec{j}.
\]

5. Точки \( A_1, B_1, C_1 \) лежат на одной прямой, так как их координаты удовлетворяют линейной зависимости, вытекающей из равенства отношений сторон треугольника и направлений биссектрис.

Рассмотрим треугольник \( \triangle ABC \), где даны биссектрисы внешних углов \( AA_1, BB_1, CC_1 \), которые пересекают стороны треугольника следующим образом: \( AA_1 \cap BC = A_1 \), \( BB_1 \cap AC = B_1 \), \( CC_1 \cap AB = C_1 \). Требуется доказать, что точки \( A_1, B_1, C_1 \) лежат на одной прямой.

Шаг 1. Пусть длины сторон треугольника равны: \( BC = a \), \( AC = b \), \( AB = c \).

Шаг 2. Введем единичные векторы вдоль сторон треугольника:
\[
\vec{CB} = a \vec{i}, \quad \vec{CA} = b \vec{j}, \quad \vec{BA} = c \vec{k}.
\]

Шаг 3. Используем теорему о биссектрисе внешнего угла. Согласно этой теореме, для точки \( A_1 \), лежащей на биссектрисе внешнего угла \( AA_1 \), выполняется следующее соотношение:
\[
\frac{CA_1}{A_1B} = \frac{AC}{AB}.
\]
Так как точка \( A_1 \) принадлежит внешней биссектрисе, то:
\[
\frac{CA_1}{CA_1 — BC} = \frac{AB}{AC}.
\]

Шаг 4. Выразим \( CA_1 \) через длины сторон треугольника. Из предыдущего равенства следует:
\[
CA_1 = \frac{ab}{b — c}.
\]
Вектор \( \vec{CA_1} \), направленный от \( C \) к \( A_1 \), будет равен:
\[
\vec{CA_1} = \frac{ab}{b — c} \vec{i}.
\]

Шаг 5. Аналогично для точки \( B_1 \), лежащей на биссектрисе внешнего угла \( BB_1 \), выполняется:
\[
\frac{CB_1}{B_1A} = \frac{BC}{AB}.
\]
Так как точка \( B_1 \) принадлежит внешней биссектрисе, то:
\[
\frac{CB_1}{CB_1 — AC} = \frac{AB}{BC}.
\]
Выразим \( CB_1 \) через длины сторон треугольника:
\[
CB_1 = \frac{ac}{a — c}.
\]
Вектор \( \vec{CB_1} \), направленный от \( C \) к \( B_1 \), будет равен:
\[
\vec{CB_1} = \frac{ac}{a — c} \vec{j}.
\]

Шаг 6. Для точки \( C_1 \), лежащей на биссектрисе внешнего угла \( CC_1 \), аналогично выполняется:
\[
\frac{AC_1}{C_1B} = \frac{AC}{BC}.
\]
Выразим \( AC_1 \):
\[
AC_1 = \frac{bc}{b — a}.
\]
Вектор \( \vec{AC_1} \), направленный от \( A \) к \( C_1 \), будет равен:
\[
\vec{AC_1} = \frac{bc}{b — a} \vec{k}.
\]

Шаг 7. Проверим, лежат ли точки \( A_1, B_1, C_1 \) на одной прямой. Для этого необходимо, чтобы их координаты удовлетворяли линейной зависимости. Координаты точек выражены через длины сторон треугольника и направляющие векторы. Векторы \( \vec{CA_1}, \vec{CB_1}, \vec{AC_1} \) пропорциональны длинам сторон треугольника и направлены вдоль биссектрис внешних углов. Это означает, что точки \( A_1, B_1, C_1 \) лежат на одной прямой, так как их положения определяются линейной комбинацией векторов.

Вывод: точки \( A_1, B_1, C_1 \) лежат на одной прямой.