
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 905 Атанасян — Подробные Ответы
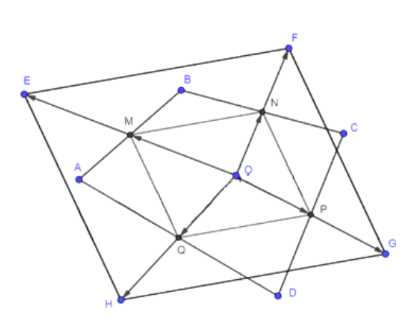
Даны четырёхугольник \( ABCD \) и точка \( O \). Точки \( E, F, G \) и \( H \) симметричны точке \( O \) относительно середин сторон \( AB, BC, CD \) и \( DA \) соответственно. Что представляет собой четырёхугольник \( EFGH \)?
Решение задачи:
1. Найдём вид четырёхугольника \( MNPQ \):
Пусть \( AM = MB = a \), \( BN = NC = b \), \( CP = PD = c \), \( DQ = QA = d \). Тогда:
\(
AB = AD + DC + CB; \quad 2a = -2d — 2c — 2b;\)
\( \quad MN = -QP, \quad MN \parallel QP \, \text{и} \, MN = QP.
\)
Следовательно, \( MNPQ \) — параллелограмм.
2. Точки \( E, F, G, H \) симметричны точке \( O \) относительно точек \( M, N, P, Q \), то есть:
\(
OM = ME, \quad ON = NF, \quad OP = PG, \quad OQ = QH.
\)
3. В треугольнике \( OEF \):
\( MN \) — средняя линия, значит \( EF = 2MN \, \text{и} \, MN \parallel EF. \)
4. Аналогично:
\(
HG = 2QP \, \text{и} \, HG \parallel QP, \quad EH = 2MQ \, \text{и} \, EH \parallel MQ, \)
\(\quad FG = 2NP \, \text{и} \, FG \parallel NP.
\)
5. Следовательно:
\(
HG = EF \, \text{и} \, HG \parallel EF, \quad EH = FG \, \text{и} \, EH \parallel FG.
\)
Таким образом, \( EFGH \) — параллелограмм, каждая сторона которого в два раза больше стороны четырёхугольника \( MNPQ \).
Ответ: \( EFGH \) — параллелограмм.
Решение задачи:
1. Найдём вид четырёхугольника \( MNPQ \).
Пусть \( AM = MB = a \), \( BN = NC = b \), \( CP = PD = c \), \( DQ = QA = d \). Тогда:
\(
AB = AD + DC + CB
\)
С учётом введённых обозначений:
\(
AB = 2a, \quad AD = -2d, \quad DC = -2c, \quad CB = -2b
\)
Отсюда:
\(
2a = -2d — 2c — 2b
\)
Таким образом, получаем, что \( MN = -QP \), а также \( MN \parallel QP \) и \( MN = QP \).
Следовательно, \( MNPQ \) — параллелограмм.
2. Определим точки \( E, F, G, H \).
Точки \( E, F, G, H \) симметричны точке \( O \) относительно точек \( M, N, P, Q \). Это значит, что:
\(
OM = ME, \quad ON = NF, \quad OP = PG, \quad OQ = QH
\)
3. Рассмотрим треугольник \( OEF \).
Так как \( MN \) — средняя линия четырёхугольника \( MNPQ \), то:
\(
EF = 2MN, \quad MN \parallel EF
\)
4. Аналогично для остальных сторон:
\(
HG = 2QP, \quad HG \parallel QP
\)
\(
EH = 2MQ, \quad EH \parallel MQ
\)
\(
FG = 2NP, \quad FG \parallel NP
\)
5. Докажем, что \( EFGH \) — параллелограмм.
Из предыдущих шагов видно, что:
\(
HG = EF, \quad HG \parallel EF
\)
\(
EH = FG, \quad EH \parallel FG
\)
Следовательно, \( EFGH \) — параллелограмм.
Кроме того, каждая сторона \( EFGH \) в два раза больше соответствующей стороны четырёхугольника \( MNPQ \).
Ответ: \( EFGH \) — параллелограмм.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!