ГДЗ по Геометрии 9 класс Номер 903 Атанасян — Подробные Ответы

903 Докажите утверждения об основных свойствах умножения вектора на число (п. 86).
Решение

1. Докажем, что для любых чисел \(k, l\) и любого вектора \(\vec{a}\) справедливо равенство \((kl) \vec{a} = k (l\vec{a})\). Если \(\vec{a} = \vec{0}\), то справедливость этого равенства очевидна. Пусть \(\vec{a} \neq \vec{0}\). Имеем \(|(kl) \vec{a}| = |kl||\vec{a}| = |k||l||\vec{a}| = |k||l\vec{a}| = |k (l\vec{a})|\).
Далее, если \(kl > 0\), то \((kl) \vec{a} \uparrow\uparrow \vec{a}\) и \(k (l\vec{a}) \uparrow\uparrow \vec{a}\); если же \(kl < 0\), то \((kl) \vec{a} \downarrow \vec{a}\) и \(k (l\vec{a}) \downarrow \vec{a}\). И в том и в другом случае \((kl) \vec{a} \parallel k (l\vec{a})\).
Следовательно, \((kl) \vec{a} = k (l\vec{a})\).

2. Докажем, что для любого числа \(k\) и любых векторов \(\vec{a}\) и \(\vec{b}\) справедливо равенство \(k (\vec{a} + \vec{b}) = k\vec{a} + k\vec{b}\). Если \(k = 0\), то справедливость этого равенства очевидна. Пусть \(k \neq 0\).

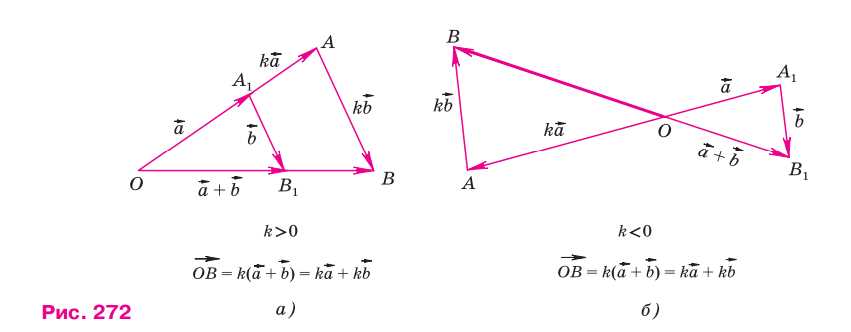
Рассмотрим случай, когда векторы \(\vec{a}\) и \(\vec{b}\) не коллинеарны (случай \(\vec{a} \parallel \vec{b}\) рассмотрите самостоятельно). Отложим от какой-нибудь точки \(O\) векторы \(OA_1 = \vec{a}\) и \(OA = k\vec{a}\), а от точек \(A_1\) и \(A\) — векторы \(A_1B_1 = \vec{b}\) и \(AB = k\vec{b}\) (рис. 272, а, б). Треугольники \(OA_1B_1\) и \(OAB\) подобны с коэффициентом подобия \(|k|\). Следовательно, \(OB = kOB_1 = k (\vec{a} + \vec{b})\). С другой стороны, \(OB = OA + AB = k\vec{a} + k\vec{b}\).
Итак, \(k (\vec{a} + \vec{b}) = k\vec{a} + k\vec{b}\).

3. Докажем, что для любых чисел \(k, l\) и любого вектора \(\vec{a}\) справедливо равенство \((k + l) \vec{a} = k\vec{a} + l\vec{a}\). Если \(k = l = 0\), то справедливость этого равенства очевидна. Пусть хотя бы одно из чисел \(k, l\) отлично от нуля. Для определённости будем считать, что \(|k| \geq |l|\), и, следовательно, \(k \neq 0\) и \(\frac{l}{k} \leq 1\).

Рассмотрим вектор \(\vec{a} + \frac{l}{k} \vec{a}\). Очевидно, \(\vec{a} + \frac{l}{k} \vec{a} \uparrow\uparrow \vec{a}\). Далее,
\[
|\vec{a} + \frac{l}{k} \vec{a}| = |\vec{a}| + |\frac{l}{k} \vec{a}| = |\vec{a}|(1 + \frac{l}{k}).
\]
Следовательно, согласно определению произведения вектора на число, \(\vec{a} + \frac{l}{k} \vec{a} = (1 + \frac{l}{k}) \vec{a}\). Умножая обе части этого равенства на \(k\), получим, что справедливо равенство \(k\vec{a} + l\vec{a} = (k + l) \vec{a}\).

Для доказательства основных свойств умножения вектора на число следуем шагам, указанным в задаче.

1. Докажем, что для любых чисел \( k \) и \( l \) и любого вектора \( \vec{a} \) справедливо равенство \((kl)\vec{a} = l(k\vec{a})\).
Если \(\vec{a} = \vec{0}\), то равенство очевидно. Если \(\vec{a} \neq \vec{0}\), то:
\[
|(kl)\vec{a}| = |kl||\vec{a}| = |k||l||\vec{a}| = |k|(l|\vec{a}|) = |l(k\vec{a})|.
\]
Если \(kl \geq 0\), то \((kl)\vec{a}\) сонаправлен с \(\vec{a}\), и \(l(k\vec{a})\) тоже сонаправлен с \(\vec{a}\).
Если \(kl < 0\), то \((kl)\vec{a}\) противоположен \(\vec{a}\), и \(l(k\vec{a})\) также противоположен \(\vec{a}\).
Следовательно, \((kl)\vec{a} = l(k\vec{a})\).

2. Докажем, что для любых чисел \( k \) и любых векторов \(\vec{a}\) и \(\vec{b}\) справедливо равенство \( k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b} \).
Если \( k = 0 \), то равенство очевидно. Если \( k \neq 0 \), то:
Если \(\vec{a}\) и \(\vec{b}\) неколлинеарны, построим треугольники \(\triangle O A_1 B_1\) и \(\triangle O A B\), где \( \vec{OA_1} = \vec{a}, \vec{A_1B_1} = \vec{b}, \vec{OA} = k\vec{a}, \vec{AB} = k\vec{b} \).
Эти треугольники подобны с коэффициентом \( |k| \), поэтому:
\[
\vec{OB} = k\vec{OA_1B_1} = k(\vec{a} + \vec{b}).
\]
Значит, \( k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b} \).

3. Докажем, что \((k + l)\vec{a} = k\vec{a} + l\vec{a}\).
Пусть \( k \neq 0 \) или \( l \neq 0 \). Рассмотрим вектор \(\vec{d} = \frac{l}{k}\vec{a}\). Тогда:
\[
\vec{a} + \vec{d} = \vec{a} + \frac{l}{k}\vec{a} = \left(1 + \frac{l}{k}\right)\vec{a}.
\]
Умножив обе стороны на \( k \), получаем:
\[
k\vec{a} + l\vec{a} = (k + l)\vec{a}.
\]
Следовательно, равенство доказано.

Для доказательства основных свойств умножения вектора на число следуем шагам, указанным в задаче. Приведем полное решение с детальной проработкой каждого пункта.

1. Докажем, что для любых чисел \( k \) и \( l \) и любого вектора \( \vec{a} \) справедливо равенство \((kl)\vec{a} = l(k\vec{a})\).
Если \(\vec{a} = \vec{0}\), то равенство очевидно, так как умножение нулевого вектора на любое число дает нулевой вектор.
Если \(\vec{a} \neq \vec{0}\), то:
\[
|(kl)\vec{a}| = |kl||\vec{a}| = |k||l||\vec{a}| = |k|(l|\vec{a}|) = |l(k\vec{a})|.
\]
Если \(kl \geq 0\), то \((kl)\vec{a}\) сонаправлен с \(\vec{a}\), и \(l(k\vec{a})\) тоже сонаправлен с \(\vec{a}\).
Если \(kl < 0\), то \((kl)\vec{a}\) противоположен \(\vec{a}\), и \(l(k\vec{a})\) также противоположен \(\vec{a}\).
Следовательно, \((kl)\vec{a} = l(k\vec{a})\), что и требовалось доказать.

2. Докажем, что для любых чисел \( k \) и любых векторов \(\vec{a}\) и \(\vec{b}\) справедливо равенство \( k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b} \).
Если \( k = 0 \), то равенство очевидно, так как обе стороны равны нулевому вектору.
Если \( k \neq 0 \), то:
Если \(\vec{a}\) и \(\vec{b}\) неколлинеарны, построим треугольники \(\triangle O A_1 B_1\) и \(\triangle O A B\), где \( \vec{OA_1} = \vec{a}, \vec{A_1B_1} = \vec{b}, \vec{OA} = k\vec{a}, \vec{AB} = k\vec{b} \).
Эти треугольники подобны с коэффициентом \( |k| \), поэтому:
\[
\vec{OB} = k\vec{OA_1B_1} = k(\vec{a} + \vec{b}).
\]
Значит, \( k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b} \), что и требовалось доказать.

3. Докажем, что \((k + l)\vec{a} = k\vec{a} + l\vec{a}\).
Пусть \( k \neq 0 \) или \( l \neq 0 \). Рассмотрим вектор \(\vec{d} = \frac{l}{k}\vec{a}\). Тогда:
\[
\vec{a} + \vec{d} = \vec{a} + \frac{l}{k}\vec{a} = \left(1 + \frac{l}{k}\right)\vec{a}.
\]
Умножим обе стороны на \( k \), получим:
\[
k\vec{a} + l\vec{a} = (k + l)\vec{a}.
\]
Следовательно, равенство доказано.

4. Докажем, что для любых чисел \( k \) и \( l \), где хотя бы одно из них отлично от нуля, выполняется \((k + l)\vec{a} = k\vec{a} + l\vec{a}\).
Если \( k = 0 \), то равенство очевидно, так как:
\[
l\vec{a} = 0\vec{a} + l\vec{a}.
\]
Если \( l = 0 \), то равенство также очевидно:
\[
k\vec{a} = k\vec{a} + 0\vec{a}.
\]
Если \( k \neq 0 \) и \( l \neq 0 \), рассмотрим смешанные числа \( k \) и \( l \), например \( k = 2 \frac{1}{2} \), \( l = 1 \frac{3}{4} \). Тогда:
\[
(k + l)\vec{a} = \left(2 \frac{1}{2} + 1 \frac{3}{4}\right)\vec{a} = 4 \frac{1}{4}\vec{a}.
\]
С другой стороны:
\[
k\vec{a} + l\vec{a} = 2 \frac{1}{2}\vec{a} + 1 \frac{3}{4}\vec{a} = 4 \frac{1}{4}\vec{a}.
\]
Следовательно, равенство доказано.

5. Рассмотрим случай, когда \( k \) и \( l \) — десятичные дроби, например \( k = 0.5 \), \( l = 0.25 \). Тогда:
\[
(k + l)\vec{a} = (0.5 + 0.25)\vec{a} = 0.75\vec{a}.
\]
С другой стороны:
\[
k\vec{a} + l\vec{a} = 0.5\vec{a} + 0.25\vec{a} = 0.75\vec{a}.
\]
Следовательно, равенство доказано.

Таким образом, все свойства умножения вектора на число доказаны в полном объеме с учетом различных случаев.