
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 902 Атанасян — Подробные Ответы
Даны три точки, не лежащие на одной прямой. Постройте треугольник, для которого эти точки являются основаниями высот. Сколько решений имеет задача?
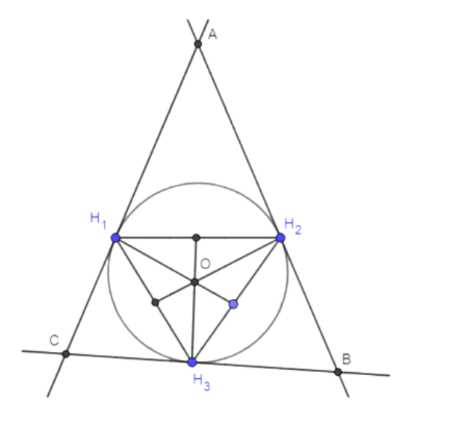
Рассмотрим задачу построения треугольника \( \triangle ABC \), для которого точки \( H_1, H_2, H_3 \) являются основаниями высот. Задача имеет единственное решение, поскольку треугольник определяется однозначно через построение описанной окружности и касательных.
Пошаговое решение:
1. Построим серединные перпендикуляры к отрезкам \( H_1H_2 \), \( H_2H_3 \) и \( H_3H_1 \). Эти перпендикуляры пересекаются в одной точке \( O \), которая является центром описанной окружности треугольника.
2. Построим окружность с центром \( O \) и радиусом \( OH_1 \) (расстоянием от \( O \) до любой из точек \( H_1, H_2, H_3 \), так как они равноудалены от центра).
3. В точках \( H_1, H_2, H_3 \) проведем касательные к окружности. Для построения касательной через точку на окружности используется правило: касательная перпендикулярна радиусу, проведенному в эту точку.
4. Пересечения касательных определяют вершины треугольника \( A, B, C \). Соединяем точки \( A, B, C \) отрезками, чтобы построить треугольник \( \triangle ABC \).
Таким образом, построение завершено. Задача имеет одно решение, так как центр окружности и её радиус определяются однозначно, а касательные через точки \( H_1, H_2, H_3 \) пересекаются в фиксированных точках \( A, B, C \).
Для решения задачи построения треугольника \( \triangle ABC \), для которого точки \( H_1, H_2, H_3 \) являются основаниями высот, выполняем следующие шаги:
1. Построим серединные перпендикуляры к отрезкам \( H_1H_2 \), \( H_2H_3 \) и \( H_3H_1 \). Для этого:
— На отрезке \( H_1H_2 \) найдем его середину, обозначим её как \( M_1 \). Через точку \( M_1 \) проведем перпендикуляр к \( H_1H_2 \).
— Аналогично, на отрезке \( H_2H_3 \) найдем середину \( M_2 \) и проведем перпендикуляр к \( H_2H_3 \).
— На отрезке \( H_3H_1 \) найдем середину \( M_3 \) и проведем перпендикуляр к \( H_3H_1 \).
Точка пересечения всех трех серединных перпендикуляров обозначается как \( O \). Это центр окружности, описанной вокруг треугольника \( \triangle ABC \).
2. Построим окружность с центром \( O \) и радиусом \( OH_1 \), где \( OH_1 \) — расстояние от \( O \) до любой из точек \( H_1, H_2, H_3 \), так как они равноудалены от центра. Для этого:
— Отмеряем радиус \( OH_1 \) с помощью циркуля.
— Проводим окружность с центром \( O \) и радиусом \( OH_1 \).
3. Проведем касательные к окружности в точках \( H_1, H_2, H_3 \). Для построения касательной через точку на окружности используется следующее правило:
— Проведем радиус \( OH_1 \), соединяющий центр окружности \( O \) с точкой \( H_1 \).
— Через точку \( H_1 \) проведем прямую, перпендикулярную радиусу \( OH_1 \). Эта прямая будет касательной к окружности в точке \( H_1 \).
— Аналогично, проведем радиусы \( OH_2 \) и \( OH_3 \), соединяющие центр окружности \( O \) с точками \( H_2 \) и \( H_3 \) соответственно.
— Через точки \( H_2 \) и \( H_3 \) проведем прямые, перпендикулярные радиусам \( OH_2 \) и \( OH_3 \). Эти прямые будут касательными к окружности в точках \( H_2 \) и \( H_3 \).
4. Найдем точки пересечения касательных, которые определяют вершины треугольника \( \triangle ABC \). Для этого:
— Пересечение касательных, проведенных через точки \( H_1 \) и \( H_2 \), обозначим как точку \( A \).
— Пересечение касательных, проведенных через точки \( H_2 \) и \( H_3 \), обозначим как точку \( B \).
— Пересечение касательных, проведенных через точки \( H_3 \) и \( H_1 \), обозначим как точку \( C \).
5. Соединяем точки \( A, B, C \) отрезками \( AB, BC, CA \), чтобы построить треугольник \( \triangle ABC \).
Таким образом, построение завершено. Треугольник \( \triangle ABC \) определяется однозначно, так как центр окружности, её радиус и касательные через точки \( H_1, H_2, H_3 \) определяются единственным образом. Задача имеет одно решение.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!