Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 901 Атанасян — Подробные Ответы
Постройте треугольник, если дана описанная окружность и на ней точки \( A \), \( B \) и \( M \), через которые проходят прямые, содержащие высоту, биссектрису и медиану треугольника, проведённые из одной вершины.
Решение задачи:
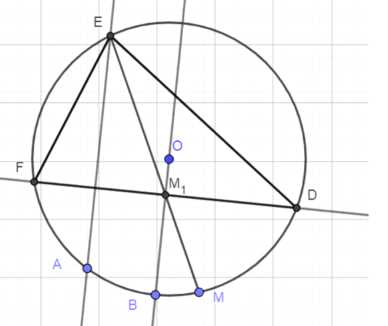
1. Через точку \( A \) проводим прямую, параллельную \( BO \). Эта прямая пересекает окружность в точке \( E \).
2. На пересечении прямых \( EM \) и \( BO \) отмечаем точку \( M_1 \).
3. Через точку \( M_1 \) строим перпендикуляр к прямой \( OB \). Этот перпендикуляр пересекает окружность в двух точках \( F \) и \( D \).
4. Соединяем точки \( A \), \( E \), \( F \) и \( D \), чтобы построить треугольник \( \triangle AEFD \).
Все построения выполняются с использованием линейки, циркуля и прямоугольного треугольника для построения перпендикуляров.
Рассмотрим задачу построения треугольника \( \triangle AEFD \) согласно условиям. Для этого выполним пошаговое построение.
1. Через точку \( A \) проведем прямую, параллельную прямой \( BO \). Для этого используем геометрическое правило построения параллельных прямых. Проведенная прямая пересекает окружность в точке \( E \). Точка \( E \) определяется как одна из двух точек пересечения прямой с окружностью.
2. Находим точку \( M_1 \), которая является точкой пересечения прямой \( EM \) с прямой \( BO \). Для этого строим прямую \( EM \), соединяющую точки \( E \) и \( M \), и определяем её пересечение с \( BO \).
3. Через точку \( M_1 \) проводим перпендикуляр к прямой \( BO \). Для этого используем правило построения перпендикуляра: через заданную точку \( M_1 \) проводится прямая, образующая угол \( 90^\circ \) с \( BO \). Этот перпендикуляр пересекает окружность в двух точках \( F \) и \( D \).
4. Соединяем точки \( A \), \( E \), \( F \) и \( D \), чтобы получить треугольник \( \triangle AEFD \). Для этого проводим отрезки \( AE \), \( EF \), \( FD \) и \( DA \), замыкающие треугольник.
Таким образом, построение завершено. Все шаги выполнены с использованием стандартных инструментов: линейки, циркуля и прямоугольного треугольника.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.