
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 899 Атанасян — Подробные Ответы
Внутри окружности дана точка. Постройте хорду, проходящую через эту точку, так, чтобы она была наименьшей из всех хорд, проходящих через эту точку.
Решение:
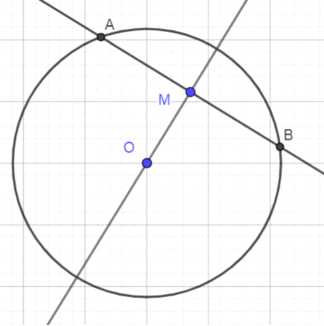
1. Проведем диаметр \( OM \), где \( O \) — центр окружности, а \( M \) — заданная точка внутри окружности.
2. Через точку \( M \) строим перпендикуляр к диаметру \( OM \).
3. Перпендикуляр пересекает окружность в двух точках \( A \) и \( B \).
4. Хорда \( AB \) является наименьшей из всех хорд, проходящих через точку \( M \).
Обоснование: минимальная хорда, проходящая через точку внутри окружности, перпендикулярна диаметру окружности, который проходит через эту точку.
Решение задачи:
1. Рассмотрим окружность с центром \( O \). Пусть внутри окружности дана точка \( M \), через которую требуется провести хорду так, чтобы она была наименьшей из всех хорд, проходящих через эту точку.
2. Для нахождения наименьшей хорды через точку \( M \) сначала проведем диаметр \( OM \). Диаметр — это прямая, соединяющая две противоположные точки окружности через её центр.
3. Построим перпендикуляр к диаметру \( OM \), проходящий через точку \( M \). Чтобы построить перпендикуляр:
— Используем циркуль для откладывания равных расстояний от точки \( M \) вдоль диаметра \( OM \).
— На концах этих отрезков строим дуги одинакового радиуса, которые пересекаются.
— Соединяем точки пересечения дуг прямой, которая будет перпендикулярной диаметру \( OM \).
4. Перпендикуляр к диаметру \( OM \) пересекает окружность в двух точках \( A \) и \( B \). Эти точки находятся на окружности и симметричны относительно точки \( M \).
5. Соединяем точки \( A \) и \( B \) отрезком. Полученная хорда \( AB \) является искомой.
Обоснование:
Для любой точки внутри окружности минимальная хорда, проходящая через эту точку, будет перпендикулярна диаметру, который проходит через эту точку. Это связано с тем, что длина хорды зависит от углов наклона её концов относительно диаметра и радиуса окружности. Перпендикулярное расположение обеспечивает минимальное расстояние между концами хорды.
Ответ: Хорда \( AB \), построенная через точку \( M \), является наименьшей.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!