
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 897 Атанасян — Подробные Ответы
Постройте общую касательную к двум данным окружностям.
Для построения общей касательной для двух окружностей выполните следующие шаги:
1. Постройте окружность с центром \( O_1 \) и радиусом \( R — r \), где \( R \) и \( r \) — радиусы двух окружностей.
2. Найдите середину отрезка \( O_1O \) и обозначьте её точкой \( M \). Постройте окружность с центром \( M \) и радиусом, равным длине отрезка \( MO \).
3. Найдите точки пересечения окружностей с центрами \( M \) и \( O_1 \). Обозначьте эти точки как \( N_1 \) и \( N_2 \).
4. Постройте перпендикуляры из точек \( O_1 \) и \( O \) к отрезкам \( N_1O \) и \( N_2O \). Точки пересечения перпендикуляров с окружностями обозначьте как \( A_1 \), \( A_2 \), \( B_1 \), и \( B_2 \).
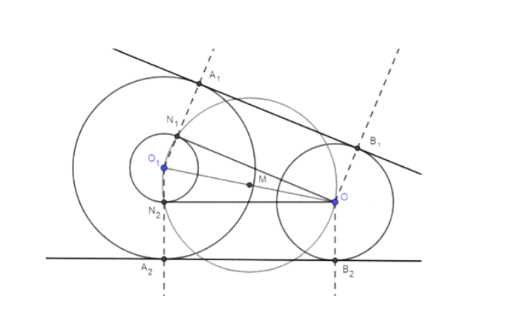
5. Постройте прямые \( A_1B_1 \) и \( A_2B_2 \). Эти прямые являются искомыми касательными.
Рассмотрим задачу построения общей касательной к двум окружностям с центрами \( O_1 \) и \( O \), радиусами \( R \) и \( r \) соответственно. Для решения задачи следуем пошаговой инструкции:
1. Построим окружность с центром в точке \( O_1 \) и радиусом \( R — r \). Эта окружность будет использована для нахождения точек пересечения с другой окружностью, которую мы построим позже.
2. Найдём середину отрезка \( O_1O \). Для этого проводим отрезок, соединяющий центры окружностей \( O_1 \) и \( O \), и делим его пополам. Обозначим середину отрезка буквой \( M \). Теперь построим окружность с центром \( M \) и радиусом, равным длине отрезка \( MO \). Радиус окружности \( MO \) равен половине расстояния между центрами окружностей \( O_1 \) и \( O \).
3. Найдём точки пересечения окружностей \( (M; MO) \) и \( (O_1; R — r) \). Для этого проведём окружности, центр которых находится в точках \( M \) и \( O_1 \), а радиусы равны \( MO \) и \( R — r \) соответственно. Обозначим точки пересечения этих окружностей как \( N_1 \) и \( N_2 \).
4. Проведём перпендикуляры из точек \( O_1 \) и \( O \) к отрезкам \( N_1O \) и \( N_2O \). Для этого из точки \( O_1 \) опускаем перпендикуляр на отрезок \( N_1O \) и обозначаем точку пересечения перпендикуляра с окружностью \( (O_1; R) \) как \( A_1 \). Аналогично, из точки \( O \) опускаем перпендикуляр на отрезок \( N_1O \) и обозначаем точку пересечения перпендикуляра с окружностью \( (O; r) \) как \( B_1 \). Повторяем аналогичные действия для отрезка \( N_2O \), обозначая точки пересечения как \( A_2 \) и \( B_2 \).
5. Построим прямые \( A_1B_1 \) и \( A_2B_2 \). Эти прямые будут являться искомыми общими касательными к данным окружностям.
Таким образом, прямые \( A_1B_1 \) и \( A_2B_2 \) — это общие касательные к двум окружностям.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!