
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 896 Атанасян — Подробные Ответы
Докажите, что основания перпендикуляров, проведённых из произвольной точки окружности, описанной около треугольника, к прямым, содержащим стороны этого треугольника, лежат на одной прямой (прямая Симсона).
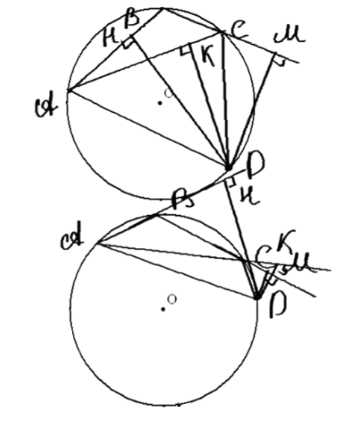
Дано: точка \( D \) — произвольная точка окружности, описанной около \( \triangle ABC \). Условие: \( DE \perp AB \), \( DG \perp CB \), \( DF \perp AC \). Требуется доказать, что точки \( E \), \( F \), \( G \) лежат на одной прямой.
Решение:
1. Рассмотрим четырехугольник \( AEFD \). Углы \( \angle AED \) и \( \angle AFD \) являются смежными, их сумма равна \( 180^\circ \). Следовательно, около четырехугольника \( AEFD \) можно описать окружность, а значит,
\(
\angle AFE = \angle ADE.
\)
2. Рассмотрим четырехугольник \( DFCG \). Углы \( \angle DFC \) и \( \angle DGC \) также смежные, их сумма равна \( 180^\circ \). Следовательно, около четырехугольника \( DFCG \) можно описать окружность, а значит,
\(
\angle CFG = \angle CDG.
\)
3. Точки \( A, B, C, D \) лежат на одной окружности, описанной около \( \triangle ABC \). Следовательно, углы \( \angle BAD \) и \( \angle BCD \) вписанные и равны:
\(
\angle BAD + \angle BCD = 180^\circ.
\)
4. Угол \( \angle DCG \) равен \( 180^\circ — \angle DCB \) по свойству смежных углов:
\(
\angle DCG = 180^\circ — \angle DCB.
\)
5. Угол \( \angle EAD \) равен \( 180^\circ — \angle BAD \), а угол \( \angle BAD \) равен \( \angle DCB \). Следовательно:
\(
\angle EAD = 180^\circ — \angle DCB = \angle DCG.
\)
6. Углы \( \angle CFG \), \( \angle CDG \), \( \angle DCG \), \( \angle EAD \), \( \angle ADE \), \( \angle AFE \) связаны следующим образом:
\(
\angle CFG = \angle AFE.
\)
Таким образом, точки \( E \), \( F \), \( G \) лежат на одной прямой, что и требовалось доказать.
Дано: точка \( D \) — произвольная точка окружности, описанной около треугольника \( \triangle ABC \). Условие: \( DE \perp AB \), \( DG \perp CB \), \( DF \perp AC \). Требуется доказать, что точки \( E \), \( F \), \( G \) лежат на одной прямой.
Решение:
1. Рассмотрим четырехугольник \( AEFD \). Углы \( \angle AED \) и \( \angle AFD \) являются смежными, их сумма равна \( 180^\circ \), так как они образуют развернутый угол вокруг точки \( D \). Следовательно, около четырехугольника \( AEFD \) можно описать окружность. Вписанный угол \( \angle AFE \) равен вписанному углу \( \angle ADE \), опирающемуся на ту же дугу. Таким образом:
\(
\angle AFE = \angle ADE.
\)
2. Рассмотрим четырехугольник \( DFCG \). Углы \( \angle DFC \) и \( \angle DGC \) также являются смежными, их сумма равна \( 180^\circ \), так как они образуют развернутый угол вокруг точки \( D \). Следовательно, около четырехугольника \( DFCG \) можно описать окружность. Вписанный угол \( \angle CFG \) равен вписанному углу \( \angle CDG \), опирающемуся на ту же дугу. Таким образом:
\(
\angle CFG = \angle CDG.
\)
3. Точки \( A \), \( B \), \( C \), \( D \) лежат на одной окружности, описанной вокруг треугольника \( \triangle ABC \). Следовательно, углы \( \angle BAD \) и \( \angle BCD \) являются вписанными углами, опирающимися на противоположные дуги окружности, и их сумма равна \( 180^\circ \):
\(
\angle BAD + \angle BCD = 180^\circ.
\)
4. Угол \( \angle DCG \) равен \( 180^\circ — \angle DCB \) по свойству смежных углов. Так как \( \angle DCB \) является вписанным углом, опирающимся на дугу \( AB \), то:
\(
\angle DCG = 180^\circ — \angle DCB.
\)
5. Угол \( \angle EAD \) является внешним углом для треугольника \( \triangle ABD \), а угол \( \angle BAD \) является внутренним углом. Следовательно,
\(
\angle EAD = 180^\circ — \angle BAD.
\)
Заменяя \( \angle BAD \) на \( \angle DCB \), так как они равны (оба опираются на одну дугу \( AB \)), получаем:
\(
\angle EAD = 180^\circ — \angle DCB.
\)
Таким образом:
\(
\angle EAD = \angle DCG.
\)
6. Углы \( \angle CFG \), \( \angle CDG \), \( \angle DCG \), \( \angle EAD \), \( \angle ADE \), \( \angle AFE \) связаны следующим образом:
\(
\angle CFG = \angle CDG = \angle DCG = \angle EAD = \angle ADE = \angle AFE.
\)
Следовательно, точки \( E \), \( F \), \( G \) лежат на одной прямой.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!