ГДЗ по Геометрии 9 класс Номер 895 Атанасян — Подробные Ответы

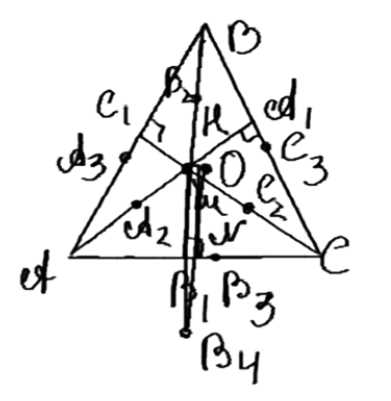
Для неравностороннего треугольника \( ABC \) точка \( O \) является центром описанной окружности, \( H \) — точка пересечения прямых, содержащих высоты \( AA_1 \), \( BB_1 \) и \( CC_1 \), точки \( A_2 \), \( B_2 \), \( C_2 \) — середины отрезков \( AH \), \( BH \), \( CH \), а точки \( A_3 \), \( B_3 \), \( C_3 \) — середины сторон треугольника \( ABC \). Докажите, что точки \( A_1 \), \( B_1 \), \( C_1 \), \( A_2 \), \( B_2 \), \( C_2 \), \( A_3 \), \( B_3 \), \( C_3 \) лежат на одной окружности (окружность Эйлера).

Дано: \( \triangle ABC \), \( O \) — центр описанной окружности (радиус \( R \)), \( H \) — точка пересечения высот \( AA_1, BB_1, CC_1 \), \( A_2, B_2, C_2 \) — середины отрезков \( AH, BH, CH \), \( A_3, B_3, C_3 \) — середины сторон \( \triangle ABC \).
Требуется доказать, что точки \( A_1, A_2, A_3, B_1, B_2, B_3, C_1, C_2, C_3 \) лежат на одной окружности.

Решение:

1. Пусть точка \( M \) — середина отрезка \( OH \). Проведем \( MN \parallel AC \).
Из теоремы Фалеса следует, что \( B_1N = NB_3 \). Также выполняется равенство \( \triangle B_1MN = \triangle B_3MN \) (по двум катетам), значит \( MB_1 = MB_3 \).

2. Пусть точка \( B_4 \) симметрична \( H \) относительно \( AC \). Рассмотрим треугольник \( \triangle OBH \):
\( MB_1 \) — средняя линия, значит
\[
MB_1 = \frac{OB}{2}.
\]
Точка \( B_4 \) лежит на окружности, описанной около \( \triangle ABC \), следовательно,
\[
MB_1 = MB_3 = \frac{R}{2}.
\]

3. Аналогично для точки \( B_2 \):
\( MB_2 \) — средняя линия \( \triangle OBH \), значит
\[
MB_2 = \frac{OB}{2} = \frac{R}{2}.
\]

4. Таким образом, \( MB_1 = MB_2 = MB_3 = \frac{R}{2} \).

5. Аналогично для точек \( A_1, A_2, A_3 \):
\[
MA_1 = MA_2 = MA_3 = \frac{R}{2}.
\]
И для точек \( C_1, C_2, C_3 \):
\[
MC_1 = MC_2 = MC_3 = \frac{R}{2}.
\]

6. Следовательно, точки \( A_1, A_2, A_3, B_1, B_2, B_3, C_1, C_2, C_3 \) лежат на одной окружности с центром в \( M \) и радиусом \( \frac{R}{2} \).

Что и требовалось доказать.

Дано: треугольник \( \triangle ABC \), \( O \) — центр описанной окружности радиуса \( R \), \( H \) — точка пересечения высот \( AA_1, BB_1, CC_1 \), \( A_2, B_2, C_2 \) — середины отрезков \( AH, BH, CH \), \( A_3, B_3, C_3 \) — середины сторон \( AB, BC, AC \). Требуется доказать, что точки \( A_1, A_2, A_3, B_1, B_2, B_3, C_1, C_2, C_3 \) лежат на одной окружности.

Решение:

1. Рассмотрим точку \( M \), которая является серединой отрезка \( OH \). Проведем отрезок \( MN \), параллельный стороне \( AC \) треугольника \( \triangle ABC \). По теореме Фалеса, отрезок \( MN \) делит \( B_1N \) и \( NB_3 \) пополам, то есть \( B_1N = NB_3 \).

2. Рассмотрим треугольники \( \triangle B_1MN \) и \( \triangle B_3MN \). Они равны как прямоугольные треугольники с равными катетами \( B_1N = NB_3 \) и общим катетом \( MN \). Следовательно, их гипотенузы также равны, то есть
\[
MB_1 = MB_3.
\]

3. Теперь рассмотрим точку \( B_4 \), которая симметрична точке \( H \) относительно стороны \( AC \). В треугольнике \( \triangle OBH \) отрезок \( MB_1 \) является средней линией, соединяющей середины двух сторон треугольника. По свойству средней линии,
\[
MB_1 = \frac{OB}{2}.
\]
Поскольку точка \( B_4 \) лежит на окружности, описанной около треугольника \( \triangle ABC \), радиус этой окружности равен \( R \). Следовательно,
\[
MB_1 = MB_3 = \frac{R}{2}.
\]

4. Аналогично рассмотрим точку \( B_2 \), которая является серединой отрезка \( BH \). В треугольнике \( \triangle OBH \) отрезок \( MB_2 \) также является средней линией, соединяющей середины двух сторон треугольника. По свойству средней линии,
\[
MB_2 = \frac{OB}{2}.
\]
Поскольку \( OB = R \), то
\[
MB_2 = \frac{R}{2}.
\]

5. Таким образом, для всех точек \( B_1, B_2, B_3 \) выполняется равенство:
\[
MB_1 = MB_2 = MB_3 = \frac{R}{2}.
\]

6. Аналогично для точек \( A_1, A_2, A_3 \), которые являются серединами отрезков \( AA_1, AH, AB \), выполняется равенство:
\[
MA_1 = MA_2 = MA_3 = \frac{R}{2}.
\]

7. Точно так же для точек \( C_1, C_2, C_3 \), которые являются серединами отрезков \( CC_1, CH, AC \), выполняется равенство:
\[
MC_1 = MC_2 = MC_3 = \frac{R}{2}.
\]

8. Таким образом, точки \( A_1, A_2, A_3, B_1, B_2, B_3, C_1, C_2, C_3 \) находятся на одинаковом расстоянии \( \frac{R}{2} \) от точки \( M \), которая является центром окружности. Следовательно, эти точки лежат на одной окружности радиуса \( \frac{R}{2} \).

Что и требовалось доказать.