
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 894 Атанасян — Подробные Ответы
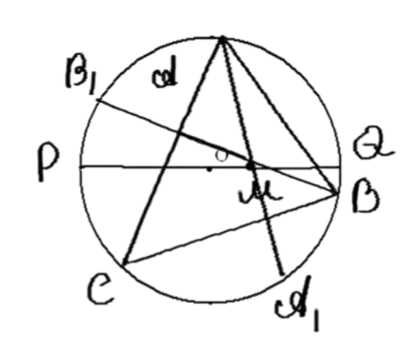
Докажите, что в любом треугольнике радиус \( R \) описанной окружности, радиус \( r \) вписанной окружности и расстояние \( d \) между центрами этих окружностей связаны равенством \( d^2 = R^2 — 2Rr \) (формула Эйлера).
Дано: треугольник \( \triangle ABC \), окружность с центром \( M \) и радиусом \( r \), окружность с центром \( O \) и радиусом \( R \), расстояние между центрами окружностей \( d = OM \). Требуется доказать: \( d^2 = R^2 — 2Rr \).
Решение:
1. Проведем через точку \( M \) диаметр описанной окружности \( PQ \), а также биссектрисы \( AM \) и \( BM \).
2. По теореме о произведении отрезков пересекающихся хорд:
\(
PM \cdot MQ = AM \cdot MA_1,
\)
где \( PM = R + d \), \( MQ = R — d \). Тогда:
\(
(R + d)(R — d) = AM \cdot MA_1.
\)
3. Так как \( AA_1 \) и \( BB_1 \) — биссектрисы, то:
\(
\angle BMA_1 = \frac{\angle BA_1 + \angle AB_1}{2}.
\)
Следовательно, треугольник \( \triangle AMA_1B \) равнобедренный.
4. Из равнобедренности треугольника:
\(
(R + d)(R — d) = AM \cdot BA_1.
\)
5. Проведем диаметр \( A_1A_2 \) описанной окружности. Пусть \( K \) — точка касания вписанной окружности со стороной \( AB \).
6. Треугольник \( \triangle A_1A_2B \) прямоугольный (так как опирается на диаметр), треугольник \( \triangle AMK \) также прямоугольный. Из подобия треугольников:
\(
\frac{MK}{BA_1} = \frac{AM}{A_1A_2},
\)
а также:
\(
\frac{r}{BA_1} = \frac{AM}{2R}.
\)
7. Подставим:
\(
AM \cdot BA_1 = 2Rr.
\)
Тогда:
\(
(R + d)(R — d) = 2Rr.
\)
Раскроем скобки:
\(
R^2 — d^2 = 2Rr.
\)
Отсюда:
\(
d^2 = R^2 — 2Rr.
\)
Что и требовалось доказать.
Дано: треугольник \( \triangle ABC \), окружность с центром \( M \) и радиусом \( r \), окружность с центром \( O \) и радиусом \( R \), расстояние между центрами окружностей \( d = OM \). Требуется доказать: \( d^2 = R^2 — 2Rr \).
Решение:
1. Проведем через точку \( M \) диаметр описанной окружности \( PQ \), а также биссектрисы \( AM \) и \( BM \). Диаметр \( PQ \) проходит через центр \( M \), а биссектрисы \( AM \) и \( BM \) делят углы треугольника \( \triangle ABC \).
2. Применим теорему о произведении отрезков пересекающихся хорд:
\(
PM \cdot MQ = AM \cdot MA_1,
\)
где \( PM = R + d \), \( MQ = R — d \). Тогда:
\(
(R + d)(R — d) = AM \cdot MA_1.
\)
Раскроем скобки:
\(
R^2 — d^2 = AM \cdot MA_1.
\)
3. Так как \( AA_1 \) и \( BB_1 \) — биссектрисы, то угол между биссектрисами \( AM \) и \( BM \) равен половине суммы углов \( \angle BA_1 \) и \( \angle AB_1 \):
\(
\angle BMA_1 = \frac{\angle BA_1 + \angle AB_1}{2}.
\)
Следовательно, треугольник \( \triangle AMA_1B \) равнобедренный.
4. Из равнобедренности треугольника \( \triangle AMA_1B \) следует, что:
\(
(R + d)(R — d) = AM \cdot BA_1.
\)
Таким образом, произведение радиусов описанной окружности и расстояния между центрами связано с длиной биссектрисы \( AM \) и отрезком \( BA_1 \).
5. Проведем диаметр \( A_1A_2 \) описанной окружности. Пусть \( K \) — точка касания вписанной окружности со стороной \( AB \). Треугольник \( \triangle A_1A_2B \) прямоугольный, так как опирается на диаметр \( A_1A_2 \), а треугольник \( \triangle AMK \) также прямоугольный.
6. Рассмотрим подобие треугольников \( \triangle AMK \) и \( \triangle A_1A_2B \). Из подобия следует:
\(
\frac{MK}{BA_1} = \frac{AM}{A_1A_2}.
\)
Кроме того, известно, что:
\(
\frac{r}{BA_1} = \frac{AM}{2R}.
\)
Таким образом, из пропорции можно выразить связь между радиусами окружностей \( r \) и \( R \), а также длиной отрезков \( BA_1 \) и \( AM \).
7. Подставим значение \( AM \cdot BA_1 = 2Rr \) в уравнение из пункта 2:
\(
(R + d)(R — d) = 2Rr.
\)
Раскроем скобки:
\(
R^2 — d^2 = 2Rr.
\)
Отсюда:
\(
d^2 = R^2 — 2Rr.
\)
Таким образом, доказательство завершено. Полученное выражение \( d^2 = R^2 — 2Rr \) соответствует условиям задачи и подтверждает связь между радиусами окружностей \( R \) и \( r \), а также расстоянием между их центрами \( d \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!