ГДЗ по Геометрии 9 класс Номер 893 Атанасян — Подробные Ответы

Докажите, что в любом четырёхугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея).

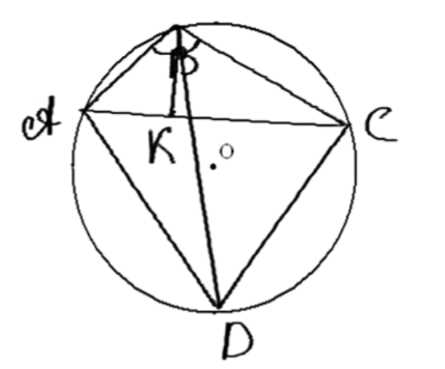
Рассмотрим доказательство, представленное в изображении.

1. На диагонали \(AC\) отметим точку \(E\), такую, что \(\angle ABE = \angle DBC\).

2. Из условия \(\angle ABE = \angle DBC\) и \(\angle BAE = \angle BCD = \frac{1}{2} \angle BCD\), следует, что \(\triangle ABE \sim \triangle DBC\) (по двум углам). Таким образом, из подобия треугольников:
\[
\frac{AB}{BD} = \frac{AE}{CD}.
\]
Умножив на \(BD \cdot CD\), получаем:
\[
AB \cdot CD = AE \cdot BD.
\]

3. Аналогично, \(\angle BCE = \angle BDA\), \(\angle EBC = \angle ABD = \angle ABE + \angle EBD\). Из этого следует, что \(\triangle BCE \sim \triangle BDA\) (по двум углам). Тогда:
\[
\frac{BC}{BD} = \frac{CE}{AD}.
\]
Умножив на \(BD \cdot AD\), получаем:
\[
BC \cdot AD = CE \cdot BD.
\]

4. Складываем два полученных равенства:
\[
AB \cdot CD + BC \cdot AD = AE \cdot BD + CE \cdot BD.
\]
Выносим \(BD\) за скобки:
\[
AB \cdot CD + BC \cdot AD = (AE + CE) \cdot BD.
\]

5. Заметим, что \(AE + CE = AC\). Подставляем:
\[
AB \cdot CD + BC \cdot AD = AC \cdot BD.
\]

Доказательство завершено.

Дано: четырехугольник \(ABCD\). Требуется доказать равенство:
\[
AC \cdot BD = AB \cdot CD + BC \cdot AD.
\]

Рассмотрим доказательство по шагам.

1. На диагонали \(AC\) отметим точку \(E\), такую, что \(\angle ABE = \angle DBC\). Это условие создаёт определённое соотношение углов между треугольниками \(ABE\) и \(DBC\).

2. Рассмотрим треугольники \(ABE\) и \(DBC\). По условию:
\[
\angle ABE = \angle DBC, \quad \angle BAE = \angle BCD.
\]
Следовательно, треугольники \(ABE\) и \(DBC\) подобны по двум углам (\(\triangle ABE \sim \triangle DBC\)). Из подобия следует пропорция:
\[
\frac{AB}{BD} = \frac{AE}{CD}.
\]
Умножим обе части на \(BD \cdot CD\), чтобы избавиться от дробей:
\[
AB \cdot CD = AE \cdot BD.
\]

3. Теперь рассмотрим треугольники \(BCE\) и \(BDA\). По условию:
\[
\angle BCE = \angle BDA, \quad \angle EBC = \angle ABD.
\]
Таким образом, треугольники \(BCE\) и \(BDA\) также подобны (\(\triangle BCE \sim \triangle BDA\)). Из подобия следует пропорция:
\[
\frac{BC}{BD} = \frac{CE}{AD}.
\]
Умножим обе части на \(BD \cdot AD\):
\[
BC \cdot AD = CE \cdot BD.
\]

4. Теперь сложим два полученных равенства:
\[
AB \cdot CD + BC \cdot AD = AE \cdot BD + CE \cdot BD.
\]
Вынесем \(BD\) за скобки в правой части:
\[
AB \cdot CD + BC \cdot AD = (AE + CE) \cdot BD.
\]

5. Заметим, что \(AE + CE = AC\) (поскольку точка \(E\) лежит на диагонали \(AC\)). Подставим это в выражение:
\[
AB \cdot CD + BC \cdot AD = AC \cdot BD.
\]

Таким образом, доказано, что:
\[
AC \cdot BD = AB \cdot CD + BC \cdot AD.
\]