ГДЗ по Геометрии 9 класс Номер 891 Атанасян — Подробные Ответы

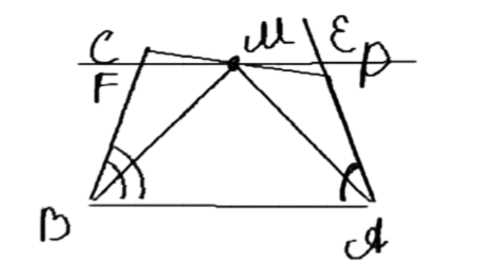
891 В четырёхугольнике ABCD, вписанном в окружность, биссектрисы углов А и В пересекаются в точке, лежащей на стороне CD. Докажите, что CD = BC + AD.

Дано: \(ABCD\) — четырехугольник, \(AE\) и \(BE\) — биссектрисы, \(E \in CD\).
Требуется доказать: \(CD = BC + AD\).

Решение:

1. Проведем \(MK \parallel AB\), где \(M \in AD\), \(K \in BC\), \(E \in MK\).

2. Угол \(\angle MEA = \frac{1}{2} \angle A\) (как накрест лежащие углы), значит треугольник \(\triangle AME\) равнобедренный. Следовательно, \(ME = MA\).

3. Угол \(\angle KEB = \frac{1}{2} \angle B\) (как накрест лежащие углы), значит треугольник \(\triangle BKE\) равнобедренный. Следовательно, \(KE = KB\).

4. Четырехугольник \(ABCD\) вписанный, следовательно:
\[
\angle AME = 180^\circ — 2 \cdot \frac{1}{2} \angle A = 180^\circ — \angle A = \angle C.
\]

5. Треугольники \(\triangle DME \sim \triangle KCE\) по двум углам.

6. Точка \(E\) — точка пересечения биссектрис, она равноудалена от \(AD\) и \(BC\). Следовательно, в треугольниках \(\triangle DME\) и \(\triangle KCE\) высоты равны, а площади одинаковы. Значит, \(DM = KC\), \(DE = KE\), \(ME = CE\).

7. Запишем длину стороны \(CD\):
\[
CD = CE + DE = ME + KE = MA + KB.
\]
Подставим \(MA = AD\) и \(KB = BC\):
\[
CD = AD + BC.
\]

Что и требовалось доказать.

Дано: \(ABCD\) — четырехугольник, \(AE\) и \(BE\) — биссектрисы углов \(A\) и \(B\), точка \(E\) лежит на стороне \(CD\). Требуется доказать, что \(CD = BC + AD\).

Решение:

1. Проведем прямую \(MK \parallel AB\), где \(M \in AD\), \(K \in BC\), \(E \in MK\). Это делается для того, чтобы использовать свойства параллельных прямых и равенства углов. Так как \(MK \parallel AB\), то углы, образованные пересечением \(MK\) с \(AD\) и \(BC\), будут равны соответствующим углам при вершинах \(A\) и \(B\).

2. Рассмотрим угол \(\angle MEA\). Так как \(MK \parallel AB\), то \(\angle MEA = \frac{1}{2} \angle A\) (накрест лежащие углы между биссектрисой и параллельной прямой). Следовательно, треугольник \(\triangle AME\) равнобедренный, так как биссектриса делит угол пополам, а \(MK \parallel AB\) создает симметрию. Из равнобедренности следует, что \(ME = MA\).

3. Аналогично рассмотрим угол \(\angle KEB\). Так как \(MK \parallel AB\), то \(\angle KEB = \frac{1}{2} \angle B\) (накрест лежащие углы). Следовательно, треугольник \(\triangle BKE\) равнобедренный, и из этого следует, что \(KE = KB\).

4. Четырехугольник \(ABCD\) является вписанным, так как его противоположные углы дополняют друг друга до \(180^\circ\). Поэтому угол \(\angle AME\) можно выразить через угол \(\angle A\):
\[
\angle AME = 180^\circ — 2 \cdot \frac{1}{2} \angle A = 180^\circ — \angle A = \angle C.
\]

5. Докажем подобие треугольников \(\triangle DME\) и \(\triangle KCE\). Для этого достаточно показать, что у них два угла равны. Первый угол \(\angle DME = \angle KCE\), так как они вертикальные. Второй угол \(\angle MDE = \angle CKE\), так как они накрест лежащие. Следовательно, \(\triangle DME \sim \triangle KCE\) по двум углам.

6. Точка \(E\) является точкой пересечения биссектрис углов \(A\) и \(B\). Это означает, что \(E\) равноудалена от сторон \(AD\) и \(BC\). Следовательно, высоты, проведенные из точки \(E\) на стороны \(AD\) и \(BC\) в треугольниках \(\triangle DME\) и \(\triangle KCE\), равны. Это приводит к равенству площадей треугольников \(\triangle DME\) и \(\triangle KCE\). Из этого следует, что \(DM = KC\), \(DE = KE\), \(ME = CE\).

7. Теперь выразим длину стороны \(CD\) через отрезки:
\[
CD = CE + DE.
\]
Подставим равенства \(CE = ME\) и \(DE = KE\):
\[
CD = ME + KE.
\]
Далее, из равенств \(ME = MA\) и \(KE = KB\), получаем:
\[
CD = MA + KB.
\]
Так как \(MA = AD\) и \(KB = BC\), то:
\[
CD = AD + BC.
\]

Таким образом, доказано, что \(CD = BC + AD\).