ГДЗ по Геометрии 9 класс Номер 890 Атанасян — Подробные Ответы

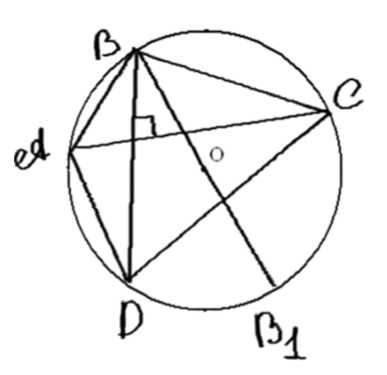
Докажите, что если диагонали вписанного четырёхугольника перпендикулярны, то сумма квадратов противоположных сторон четырёхугольника равна квадрату диаметра описанной окружности. 

Дано: четырехугольник \(ABCD\), диагонали \(AC\) и \(BD\) пересекаются под прямым углом.
Требуется доказать: \(AB^2 + CD^2 = AD^2 + BC^2 = (2R)^2\), где \(R\) — радиус описанной окружности.

Решение:

1. Отметим точку пересечения диагоналей \(E = AC \cap BD\).

2. По теореме Пифагора:
\(
AB^2 + CD^2 = AE^2 + BE^2 + DE^2 + CE^2,\)

\(AD^2 + BC^2 = AE^2 + DE^2 + BE^2 + CE^2.
\)

3. Проведем диаметр \(AA’\) окружности, описанной вокруг четырехугольника \(ABCD\).

4. Треугольники \(DBA’\) и \(CDA’\) прямоугольные, так как опираются на диаметр окружности. Углы:
\(
\angle DBA’ = 90^\circ — \angle ABD, \quad \angle CDA’ = 90^\circ — \angle ACD.
\)
Следовательно, \(\angle DBA’ = \angle CDB\).

5. Рассмотрим треугольники \(DBC\) и \(BDA’\).
Углы:
\(
\angle DCB = \angle BA’D, \quad \angle CDB = \angle DBA’.
\)
Общая сторона \(DB\), следовательно, треугольники \(DBC\) и \(BDA’\) равны. Тогда:
\(
BA’ = CD.
\)

6. В треугольнике \(ABA’\):
\(
AA’^2 = AB^2 + BA’^2 = AB^2 + CD^2 = (2R)^2.
\)

Таким образом, доказано, что \(AB^2 + CD^2 = AD^2 + BC^2 = (2R)^2\), что и требовалось доказать.

Дано: четырехугольник \(ABCD\), диагонали \(AC\) и \(BD\) пересекаются под прямым углом.
Требуется доказать: \(AB^2 + CD^2 = AD^2 + BC^2 = (2R)^2\), где \(R\) — радиус описанной окружности.

Решение:

1. Обозначим точку пересечения диагоналей \(E = AC \cap BD\). Диагонали пересекаются под прямым углом, то есть \(\angle AEB = \angle CED = 90^\circ\).

2. Рассмотрим теорему Пифагора для четырёхугольника.
Сумма квадратов двух противоположных сторон выражается через длины отрезков диагоналей:
\(
AB^2 + CD^2 = AE^2 + BE^2 + DE^2 + CE^2.
\)
Аналогично для другой пары противоположных сторон:
\(
AD^2 + BC^2 = AE^2 + DE^2 + BE^2 + CE^2.
\)

3. Проведём диаметр \(AA’\) окружности, описанной вокруг четырёхугольника \(ABCD\). Точки \(A\), \(B\), \(C\), \(D\) лежат на окружности, а диаметр \(AA’\) проходит через центр окружности.

4. Рассмотрим треугольники \(DBA’\) и \(CDA’\). Эти треугольники прямоугольные, так как их гипотенузы опираются на диаметр окружности. Углы при вершинах:
\(
\angle DBA’ = 90^\circ — \angle ABD, \quad \angle CDA’ = 90^\circ — \angle ACD.
\)
Из этого следует, что углы \(\angle DBA’\) и \(\angle CDB\) равны.

5. Рассмотрим треугольники \(DBC\) и \(BDA’\).
В этих треугольниках:
\(
\angle DCB = \angle BA’D, \quad \angle CDB = \angle DBA’.
\)
Кроме того, они имеют общую сторону \(DB\). Следовательно, треугольники \(DBC\) и \(BDA’\) равны по двум углам и стороне. Из равенства треугольников следует:
\(
BA’ = CD.
\)

6. Теперь рассмотрим треугольник \(ABA’\), который также является прямоугольным, так как \(AA’\) — диаметр окружности. По теореме Пифагора:
\(
AA’^2 = AB^2 + BA’^2.
\)
Подставим \(BA’ = CD\):
\(
AA’^2 = AB^2 + CD^2.
\)

7. Диаметр окружности равен \(2R\), где \(R\) — радиус описанной окружности. Тогда:
\(
AA’^2 = (2R)^2.
\)

Таким образом, доказано, что:
\(
AB^2 + CD^2 = (2R)^2.
\)

Аналогично можно доказать, что:
\(
AD^2 + BC^2 = (2R)^2.
\)

Итог: \(AB^2 + CD^2 = AD^2 + BC^2 = (2R)^2\), что и требовалось доказать.