
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 889 Атанасян — Подробные Ответы
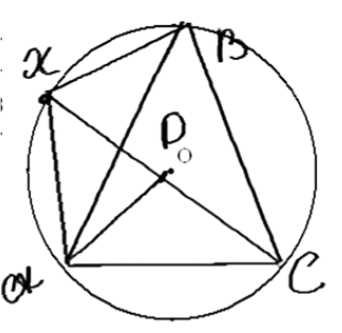
Произвольная точка \( X \) окружности, описанной около равностороннего треугольника \( ABC \), соединена отрезками с его вершинами. Докажите, что один из отрезков \( AX \), \( BX \) и \( CX \) равен сумме двух других отрезков.
Дано: треугольник \( \triangle ABC \) — равносторонний; точка \( X \) принадлежит стороне \( AB \).
Требуется доказать: \( XC = XA + XB \).
Рассмотрим решение задачи.
1. Отложим на отрезке \( XC \) отрезок \( XD = XA \).
2. Треугольник \( \triangle AXD \) равнобедренный, так как \( XA = XD \), а угол \( \angle AXD = \angle ABC = \frac{1}{2} \cdot \angle AC = 60^\circ \). Следовательно, треугольник \( \triangle AXD \) равносторонний:
\[
XA = XD, \quad \angle AXD = \angle DAX = 60^\circ.
\]
3. Рассмотрим треугольники \( \triangle ADC \) и \( \triangle AXB \).
Из условия задачи \( AC = AB \), \( AD = AX \), угол \( \angle CAD = \angle BAX = 60^\circ — \angle DAB \). Следовательно, треугольники \( \triangle ADC \) и \( \triangle AXB \) равны по двум сторонам и углу между ними:
\[
\triangle ADC = \triangle AXB.
\]
Отсюда следует, что \( DC = XB \).
4. Теперь вычислим длину \( XC \):
\[
XC = XD + DC = XA + XB.
\]
Таким образом, доказано, что \( XC = XA + XB \), что и требовалось доказать.
Дано: треугольник \( \triangle ABC \) является равносторонним, точка \( X \) принадлежит стороне \( AB \).
Требуется доказать: \( XC = XA + XB \).
Рассмотрим решение задачи.
1. На отрезке \( XC \) отложим точку \( D \), такую что \( XD = XA \). Это возможно, так как длина \( XC \) больше или равна длине \( XA \).
2. Рассмотрим треугольник \( \triangle AXD \).
Из условия задачи угол \( \angle AXD \) равен углу \( \angle ABC \), так как \( \triangle ABC \) равносторонний. Следовательно:
\[
\angle AXD = \angle ABC = \frac{1}{2} \cdot \angle AC = 60^\circ.
\]
В треугольнике \( \triangle AXD \) две стороны равны (\( XA = XD \)) и один угол между ними равен \( 60^\circ \). Это значит, что треугольник \( \triangle AXD \) равносторонний. Тогда:
\[
XA = XD, \quad \angle AXD = \angle DAX = 60^\circ.
\]
3. Рассмотрим треугольники \( \triangle ADC \) и \( \triangle AXB \).
Из условия задачи известно, что \( AC = AB \) (так как треугольник \( \triangle ABC \) равносторонний), а также \( AD = AX \) (по построению, так как \( \triangle AXD \) равносторонний). Углы \( \angle CAD \) и \( \angle BAX \) равны, так как каждый из них равен \( 60^\circ — \angle DAB \). Таким образом, треугольники \( \triangle ADC \) и \( \triangle AXB \) равны по двум сторонам и углу между ними. Следовательно:
\[
\triangle ADC = \triangle AXB, \quad DC = XB.
\]
4. Теперь вычислим длину \( XC \). Используем разбиение отрезка \( XC \) на два отрезка:
\[
XC = XD + DC.
\]
Подставим значения: \( XD = XA \), \( DC = XB \):
\[
XC = XA + XB.
\]
Таким образом, доказано, что \( XC = XA + XB \), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!