ГДЗ по Геометрии 9 класс Номер 886 Атанасян — Подробные Ответы

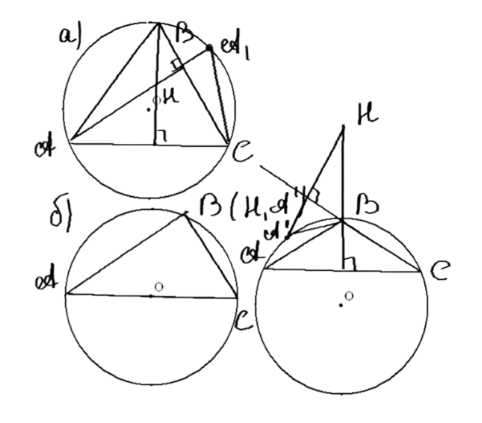
Пусть \( H \) — точка пересечения прямых, содержащих высоты треугольника \( ABC \), а \( A’ \), \( B’ \), \( C’ \) — точки, симметричные точке \( H \) относительно прямых \( BC \), \( CA \), \( AB \). Докажите, что точки \( A’ \), \( B’ \), \( C’ \) лежат на окружности, описанной около треугольника \( ABC \).  

Дано: треугольник \( \triangle ABC \), точка пересечения высот \( H \), точки \( A’, B’, C’ \) — симметричны \( A, B, C \) относительно \( H \).
Требуется доказать, что точки \( A’, B’, C’ \) лежат на описанной окружности треугольника \( \triangle ABC \).

Решение:

1. Докажем, что \( A’ \) лежит на окружности, описанной около \( \triangle ABC \).
Если треугольник остроугольный (\( \angle B < 90^\circ \)), то угол \( \angle CBA’ = \angle CBH = 90^\circ — \angle C \). Следовательно, угол \( \angle ABA’ = 90^\circ — \angle C + \angle B \). Аналогично угол \( \angle ACA’ = 90^\circ — \angle B + \angle C \). Таким образом, в четырехугольнике \( ABA’C \) сумма противоположных углов равна \( \angle ABA’ + \angle ACA’ = 180^\circ \), следовательно, вокруг него можно описать окружность. Так как точки \( A, B, C \) принадлежат одной окружности, то \( A’ \) также принадлежит этой окружности.

2. Аналогично для \( B’ \) и \( C’ \): можно показать, что \( B’ \) и \( C’ \) также принадлежат окружности, описанной около \( \triangle ABC \).

3. Если треугольник прямоугольный (\( \angle B = 90^\circ \)), то точка пересечения высот совпадает с точкой \( H \), а значит \( A’ = C’ = H = B \). Таким образом, точки \( A’, B’, C’ \) лежат на описанной окружности треугольника \( \triangle ABC \).

4. Если треугольник тупоугольный (\( \angle B > 90^\circ \)), то угол \( \angle AA’B = 180^\circ — \angle HA’B = 180^\circ — \angle BHA’ \), где \( \angle BHA’ = 90^\circ — \angle CAH = \angle C \). Таким образом, в четырехугольнике \( AA’BC \) сумма противоположных углов равна \( \angle A’ + \angle C = 180^\circ \), следовательно, вокруг него можно описать окружность. Так как точки \( A, B, C \) принадлежат одной окружности, то \( A’, B’, C’ \) также принадлежат этой окружности.

Вывод: точки \( A’, B’, C’ \) лежат на окружности, описанной около треугольника \( \triangle ABC \).

Дано: треугольник \( \triangle ABC \). Точка \( H \) — точка пересечения высот. Точки \( A’, B’, C’ \) — симметричны точкам \( A, B, C \) относительно точки \( H \).
Требуется доказать, что точки \( A’, B’, C’ \) лежат на окружности, описанной около треугольника \( \triangle ABC \).

Решение:

1. Рассмотрим случай, когда треугольник \( \triangle ABC \) остроугольный (\( \angle B < 90^\circ \)).
Точка \( A’ \) симметрична точке \( A \) относительно точки пересечения высот \( H \). Это означает, что \( H \) является серединой отрезка \( AA’ \).
Угол \( \angle CBA’ \) равен \( \angle CBH \), так как \( A’ \) симметрична \( A \) относительно \( H \). Поскольку \( \angle CBH = 90^\circ — \angle C \), то \( \angle CBA’ = 90^\circ — \angle C \).
Аналогично, угол \( \angle ABA’ = 90^\circ — \angle C + \angle B \).
Угол \( \angle ACA’ = 90^\circ — \angle B + \angle C \).
В четырехугольнике \( ABA’C \) сумма противоположных углов равна:
\[
\angle ABA’ + \angle ACA’ = (90^\circ — \angle C + \angle B) + (90^\circ — \angle B + \angle C) = 180^\circ.
\]
Так как сумма противоположных углов равна \( 180^\circ \), то вокруг четырехугольника \( ABA’C \) можно описать окружность. Поскольку через точки \( A, B, C \) проходит только одна окружность, описанная около треугольника \( \triangle ABC \), то \( A’ \) также лежит на этой окружности.

2. Аналогично для точки \( B’ \):
Точка \( B’ \) симметрична точке \( B \) относительно точки \( H \), поэтому \( H \) является серединой отрезка \( BB’ \).
Угол \( \angle ACB’ = \angle ACH = 90^\circ — \angle A \).
Угол \( \angle BCB’ = 90^\circ — \angle A + \angle C \).
Угол \( \angle BAB’ = 90^\circ — \angle C + \angle A \).
В четырехугольнике \( BCB’A \) сумма противоположных углов равна:
\[
\angle BCB’ + \angle BAB’ = (90^\circ — \angle A + \angle C) + (90^\circ — \angle C + \angle A) = 180^\circ.
\]
Следовательно, вокруг четырехугольника \( BCB’A \) можно описать окружность. Поскольку через точки \( A, B, C \) проходит только одна окружность, описанная около треугольника \( \triangle ABC \), то \( B’ \) также лежит на этой окружности.

3. Аналогично для точки \( C’ \):
Точка \( C’ \) симметрична точке \( C \) относительно точки \( H \), поэтому \( H \) является серединой отрезка \( CC’ \).
Угол \( \angle BAC’ = \angle BAH = 90^\circ — \angle B \).
Угол \( \angle CAC’ = 90^\circ — \angle B + \angle A \).
Угол \( \angle CBC’ = 90^\circ — \angle A + \angle B \).
В четырехугольнике \( CAC’B \) сумма противоположных углов равна:
\[
\angle CAC’ + \angle CBC’ = (90^\circ — \angle B + \angle A) + (90^\circ — \angle A + \angle B) = 180^\circ.
\]
Следовательно, вокруг четырехугольника \( CAC’B \) можно описать окружность. Поскольку через точки \( A, B, C \) проходит только одна окружность, описанная около треугольника \( \triangle ABC \), то \( C’ \) также лежит на этой окружности.

4. Рассмотрим случай, когда треугольник \( \triangle ABC \) прямоугольный (\( \angle B = 90^\circ \)).
В этом случае точка пересечения высот совпадает с вершиной \( H = B \). Тогда точки \( A’ \) и \( C’ \) симметричны \( A \) и \( C \) относительно \( B \). Это означает, что \( A’ = C’ = H = B \).
Поскольку \( \triangle ABC \) является прямоугольным, то вокруг него можно описать окружность, и все его вершины \( A, B, C \), а также симметричные точки \( A’, B’, C’ \) лежат на этой окружности.

5. Рассмотрим случай, когда треугольник \( \triangle ABC \) тупоугольный (\( \angle B > 90^\circ \)).
Угол \( \angle AA’B = 180^\circ — \angle HA’B = 180^\circ — \angle BHA’ \).
Угол \( \angle BHA’ = 90^\circ — \angle CAH = \angle C \).
Таким образом, \( \angle AA’B = 180^\circ — \angle C \).
В четырехугольнике \( AA’BC \) сумма противоположных углов равна:
\[
\angle AA’B + \angle C = (180^\circ — \angle C) + \angle C = 180^\circ.
\]
Следовательно, вокруг четырехугольника \( AA’BC \) можно описать окружность. Поскольку через точки \( A, B, C \) проходит только одна окружность, описанная около треугольника \( \triangle ABC \), то \( A’, B’, C’ \) также лежат на этой окружности.

Вывод: точки \( A’, B’, C’ \) лежат на окружности, описанной около треугольника \( \triangle ABC \), независимо от типа треугольника (\( \triangle ABC \) может быть остроугольным, прямоугольным или тупоугольным).