Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 885 Атанасян — Подробные Ответы
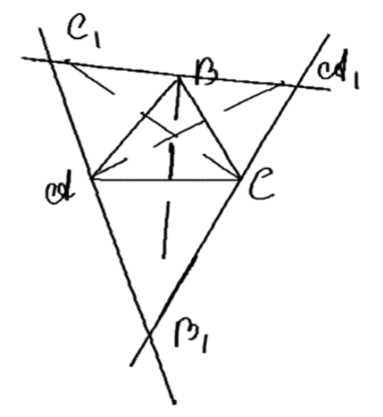
Через каждую вершину треугольника \( ABC \) проведена прямая, перпендикулярная к биссектрисе угла треугольника при этой вершине. Проведённые прямые, пересекаясь, образуют новый треугольник. Докажите, что вершины этого треугольника лежат на прямых, содержащих биссектрисы треугольника \( ABC \).
Дано:
Треугольник \( \triangle ABC \), его биссектрисы \( AA_1 \), \( BB_1 \), \( CC_1 \).
Прямые \( C_2B_2 \perp AA_2 \), \( A_2C_2 \perp BB_2 \), \( A_2B_2 \perp CC_2 \).
Доказать:
\( A_2 \in AA_1 \), \( B_2 \in BB_1 \), \( C_2 \in CC_1 \).
Решение:
1. Прямые, перпендикулярные к биссектрисам внутренних углов треугольника, являются биссектрисами соответствующих внешних углов. Следовательно:
\[
A_2B_2 \text{ — биссектриса внешнего угла } \angle C,
\]
\[
A_2C_2 \text{ — биссектриса внешнего угла } \angle B,
\]
\[
B_2C_2 \text{ — биссектриса внешнего угла } \angle A.
\]
2. Каждая точка биссектрисы угла равноудалена от сторон, которые этот угол образует. Следовательно:
\[
B_2 \in B_2C_2 \text{ и } A_2B_2, \text{ то есть } B_2 \text{ равноудалена от сторон } AB \text{ и } BC.
\]
Аналогично для точек \( A_2 \) и \( C_2 \).
3. Таким образом:
\[
A_2 \in AA_1, \quad B_2 \in BB_1, \quad C_2 \in CC_1.
\]
Что и требовалось доказать.
Дано:
Треугольник \( \triangle ABC \), его биссектрисы \( AA_1 \), \( BB_1 \), \( CC_1 \).
Прямые \( C_2B_2 \perp AA_2 \), \( A_2C_2 \perp BB_2 \), \( A_2B_2 \perp CC_2 \).
Доказать:
\( A_2 \in AA_1 \), \( B_2 \in BB_1 \), \( C_2 \in CC_1 \).
Решение:
1. Рассмотрим свойства биссектрис треугольника.
Биссектриса внутреннего угла делит угол на две равные части и проходит через одну из вершин треугольника. Прямые, перпендикулярные к биссектрисам внутренних углов, являются биссектрисами соответствующих внешних углов.
Следовательно:
\[
A_2B_2 \text{ — биссектриса внешнего угла } \angle C,
\]
\[
A_2C_2 \text{ — биссектриса внешнего угла } \angle B,
\]
\[
B_2C_2 \text{ — биссектриса внешнего угла } \angle A.
\]
2. Теперь обратимся к свойству биссектрис.
Каждая точка биссектрисы угла равноудалена от сторон, которые этот угол образуют. Это свойство справедливо как для внутренних, так и для внешних углов. Поэтому можно записать:
\[
B_2 \in B_2C_2 \text{ и } A_2B_2, \text{ то есть } B_2 \text{ равноудалена от сторон } AB \text{ и } BC.
\]
Аналогично для точек \( A_2 \) и \( C_2 \):
\[
A_2 \text{ равноудалена от сторон } AB \text{ и } AC,
\]
\[
C_2 \text{ равноудалена от сторон } BC \text{ и } AC.
\]
3. Таким образом, точки \( A_2 \), \( B_2 \), \( C_2 \) принадлежат соответствующим биссектрисам внутренних углов треугольника:
\[
A_2 \in AA_1, \quad B_2 \in BB_1, \quad C_2 \in CC_1.
\]
4. Вывод:
Доказано, что точки \( A_2 \), \( B_2 \), \( C_2 \) принадлежат биссектрисам \( AA_1 \), \( BB_1 \), \( CC_1 \).
Что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.