ГДЗ по Геометрии 9 класс Номер 883 Атанасян — Подробные Ответы

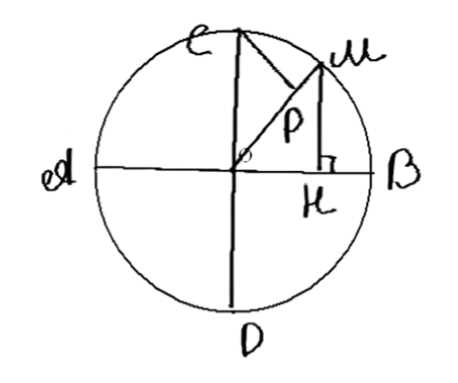
Отрезок \( AB \) является диаметром окружности с центром \( O \). На каждом радиусе \( OM \) окружности отложен от центра \( O \) отрезок, равный расстоянию от конца \( M \) этого радиуса до прямой \( AB \). Найдите множество концов построенных таким образом отрезков.

Дано:
Точка \(M\) принадлежит окружности с радиусом \(R\).
\(
AB = 2R, \quad OM = R, \quad MH \perp AB, \quad DE \parallel OM, \quad OD = MH.
\)

Решение:
1. Точка \(M\) лежит на окружности с радиусом \(R\), поэтому:
\(
OD = MH = R \cdot \sin \alpha.
\)

2. Координаты точки \(M\):
\(
x = \cos \alpha, \quad y = \sin \alpha.
\)
Подставим их в уравнение окружности для точки \(D\):
\(
x^2 + \left(y \pm \frac{1}{2}\right)^2 = \left(\frac{1}{2}\right)^2.
\)

3. Таким образом, точка \(D\) принадлежит двум окружностям с центрами:
\(
\left(0; \pm \frac{R}{2}\right)
\)
и радиусами:
\(
\frac{R}{2}.
\)

Ответ: точки \(D\) лежат на окружностях с центрами \((0; \pm R/2)\) и радиусом \(R/2\).

Дано:
Точка \(M\) принадлежит окружности с радиусом \(R\).
\(
AB = 2R, \quad OM = R, \quad MH \perp AB, \quad DE \parallel OM, \quad OD = MH.
\)

Необходимо найти множество точек \(D\).

Решение:

1. Точка \(M\) принадлежит окружности с радиусом \(R\), поэтому расстояние \(OD = MH\) можно выразить через угол \(\alpha\):
\(
OD = MH = R \cdot \sin \alpha.
\)

2. Координаты точки \(M\) на окружности задаются параметрически:
\(
x = \cos \alpha, \quad y = \sin \alpha.
\)

3. Точка \(D\) лежит на прямой \(OM\), которая параллельна оси \(y\). Поэтому ее координаты можно записать как:
\(
D(0; y_D),
\)
где \(y_D\) — координата точки \(D\) вдоль оси \(y\).

4. Согласно условию, \(OD = MH\), а \(MH\) — расстояние от точки \(M\) до прямой \(AB\). Прямая \(AB\) проходит через точку \(O(0; 0)\), а точка \(M\) имеет координаты \((\cos \alpha; \sin \alpha)\). Расстояние от точки \(M\) до прямой \(AB\) равно:
\(
MH = |y| = |\sin \alpha|.
\)
Отсюда:
\(
OD = |\sin \alpha|.
\)

5. Точка \(D\) лежит на прямой \(OM\), а \(OM\) — вертикальная прямая, проходящая через точку \(O\). Координаты точки \(D\) можно записать как:
\(
D(0; y_D),
\)
где \(y_D = \pm OD = \pm R \cdot \sin \alpha\).

6. Точка \(D\) принадлежит двум окружностям, так как ее расстояние до центра \(O(0; 0)\) фиксировано, и это расстояние равно радиусу окружности. Уравнение окружности для точки \(D\) имеет вид:
\(
x^2 + \left(y \pm \frac{R}{2}\right)^2 = \left(\frac{R}{2}\right)^2.
\)

7. Таким образом, множество точек \(D\) принадлежит двум окружностям с центрами:
\(
(0; \pm \frac{R}{2}),
\)
и радиусом:
\(
\frac{R}{2}.
\)

Ответ: точки \(D\) лежат на окружностях с центрами \((0; \pm R/2)\) и радиусом \(R/2\).