ГДЗ по Геометрии 9 класс Номер 882 Атанасян — Подробные Ответы

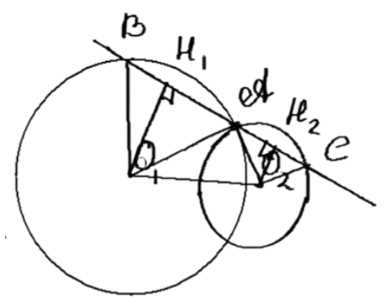
Через точку \( A \) пересечения двух окружностей с центрами в точках \( O_1 \) и \( O_2 \) проведена прямая, пересекающая одну окружность в точке \( B \), а другую — в точке \( C \). Докажите, что отрезок \( BC \) будет наибольшим тогда, когда он параллелен прямой \( O_1O_2 \). 

Рассмотрим задачу:

1. Проведем из точек \(O_1\) и \(O_2\) перпендикуляры к прямой \(BC\): \(O_1H_1 \perp BC\) и \(O_2H_2 \perp BC\).

2. Рассмотрим треугольники \(\triangle BAO_1\) и \(\triangle CAO_2\). Они равнобедренные, так как \(BO_1 = O_1A = r_1\) и \(AO_2 = O_2C = r_2\). Следовательно, высоты \(O_1H_1\) и \(O_2H_2\) являются медианами. Тогда:
\[
H_1A = \frac{1}{2}BA, \quad H_2A = \frac{1}{2}AC.
\]

3. Таким образом, длина \(BC\) выражается как:
\[
BC = 2 \cdot H_1H_2.
\]

4. Рассмотрим \(H_1H_2O_1O_2\), которая является прямоугольной трапецией. Длина \(H_1H_2\) вычисляется по формуле:
\[
H_1H_2 = \sqrt{(O_1O_2)^2 — (H_1O_1 — H_2O_2)^2}.
\]

5. \(H_1H_2\) будет максимальной, если \(H_1O_1 = H_2O_2\), так как это условие минимизирует вычитаемое \((H_1O_1 — H_2O_2)^2\). Это происходит, когда \(BC \parallel O_1O_2\).

Следовательно, \(BC\) максимально, когда \(BC \parallel O_1O_2\), что и требовалось доказать.

Рассмотрим задачу и проведем доказательство шаг за шагом.

Дано:
1. Точки \(O_1\) и \(O_2\) являются центрами окружностей.
2. Точка \(A\) лежит на прямой \(BC\).
3. \(BA\) и \(AC\) — хорды окружностей с центрами \(O_1\) и \(O_2\) соответственно.

Требуется доказать: длина \(BC\) максимальна, когда \(BC \parallel O_1O_2\).

Решение:

1. Проведем из точек \(O_1\) и \(O_2\) перпендикуляры к прямой \(BC\). Обозначим точки пересечения этих перпендикуляров с прямой \(BC\) как \(H_1\) и \(H_2\) соответственно:
\[
O_1H_1 \perp BC, \quad O_2H_2 \perp BC.
\]
Таким образом, \(H_1\) и \(H_2\) — основания перпендикуляров из \(O_1\) и \(O_2\) на прямую \(BC\).

2. Рассмотрим треугольники \(\triangle BAO_1\) и \(\triangle CAO_2\).
Эти треугольники равнобедренные, так как:
\[
BO_1 = O_1A = r_1, \quad AO_2 = O_2C = r_2,
\]
где \(r_1\) и \(r_2\) — радиусы окружностей с центрами \(O_1\) и \(O_2\).

В равнобедренных треугольниках высоты \(O_1H_1\) и \(O_2H_2\) являются медианами. Следовательно:
\[
H_1A = \frac{1}{2}BA, \quad H_2A = \frac{1}{2}AC.
\]

3. Выразим длину \(BC\):
Длина \(BC\) состоит из двух отрезков \(BH_1\) и \(H_2C\), которые равны удвоенной длине \(H_1H_2\) (расстояние между основаниями перпендикуляров):
\[
BC = 2 \cdot H_1H_2.
\]

4. Рассмотрим четырехугольник \(H_1H_2O_1O_2\).
Этот четырехугольник является прямоугольной трапецией, так как \(O_1H_1 \perp BC\) и \(O_2H_2 \perp BC\).
Выразим длину \(H_1H_2\) через элементы трапеции:
\[
H_1H_2 = \sqrt{(O_1O_2)^2 — (H_1O_1 — H_2O_2)^2}.
\]

5. Для максимизации длины \(H_1H_2\) необходимо минимизировать вычитаемое \((H_1O_1 — H_2O_2)^2\).
Минимальное значение достигается, когда:
\[
H_1O_1 = H_2O_2,
\]
то есть перпендикуляры \(O_1H_1\) и \(O_2H_2\) имеют одинаковую длину.

6. Условие равенства длин перпендикуляров выполняется, если прямая \(BC\) параллельна \(O_1O_2\):
\[
BC \parallel O_1O_2.
\]

Вывод: длина \(BC\) максимальна, когда \(BC \parallel O_1O_2\), что и требовалось доказать.