Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 880 Атанасян — Подробные Ответы
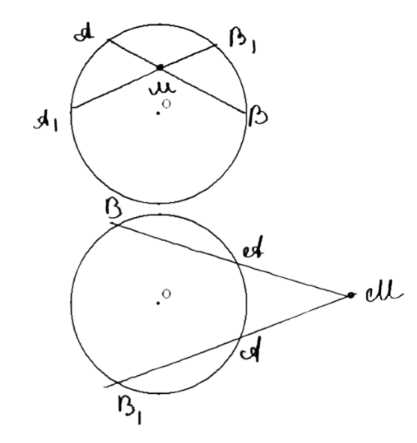
Окружность отсекает на двух прямых, которые пересекаются в точке, не лежащей на окружности, равные хорды. Докажите, что расстояния от точки пересечения этих прямых до концов той и другой хорды соответственно равны между собой.
Рассмотрим доказательство задачи:
Дано: окружность \((O; R)\), \(AB \in a\), \(CD \in b\), \(a \cap b = M\).
1. Рассмотрим треугольники \(\triangle ACM\) и \(\triangle BDM\). По условию \(AC = BD\), углы \(\angle CAB = \angle CDB = \frac{1}{2} \angle BC\), а также \(\angle ABD = \angle ACD = \frac{1}{2} \angle AD\). Следовательно, треугольники \(\triangle ACM\) и \(\triangle BDM\) равны по стороне и двум прилежащим углам. Отсюда следует, что \(MA = MD\) и \(MC = MB\).
2. Рассмотрим случай, когда \(AB = CD\). Углы \(\angle BAC = \angle BDC = \frac{1}{2} \angle BC\), \(\angle ADB = \frac{1}{2} \angle AB = \frac{1}{2} \angle CD = \angle CAD\). Следовательно, \(\angle BAC + \angle CAD = \angle BDC + \angle ADB\), отсюда \(\angle A = \angle B\). Таким образом, треугольник \(\triangle AMD\) равнобедренный, значит \(MA = MD\). Поскольку \(AB = CD\), то \(MC = MB\).
Что и требовалось доказать.
Дано: окружность \((O; R)\), \(AB \in a\), \(CD \in b\), \(a \cap b = M\). Требуется доказать, что \(MA = MD\) и \(MC = MB\).
Рассмотрим два случая:
а) \(AC = BD\) — хорды окружности.
Рассмотрим треугольники \(\triangle ACM\) и \(\triangle BDM\). По условию:
1. \(AC = BD\) — стороны треугольников равны.
2. Углы \(\angle CAB = \angle CDB = \frac{1}{2} \angle BC\) — равны, так как дуги \(AB\) и \(CD\) делятся пополам.
3. Углы \(\angle ABD = \angle ACD = \frac{1}{2} \angle AD\) — равны, так как дуги \(AB\) и \(CD\) делятся пополам.
Следовательно, треугольники \(\triangle ACM\) и \(\triangle BDM\) равны по стороне и двум прилежащим углам. Из равенства треугольников следует, что \(MA = MD\) и \(MC = MB\).
б) \(AB = CD\) — хорды окружности.
Рассмотрим углы:
1. \(\angle BAC = \angle BDC = \frac{1}{2} \angle BC\), так как дуги \(AB\) и \(CD\) делятся пополам.
2. \(\angle ADB = \frac{1}{2} \angle AB = \frac{1}{2} \angle CD = \angle CAD\), так как дуги \(AB\) и \(CD\) делятся пополам.
Следовательно, \(\angle BAC + \angle CAD = \angle BDC + \angle ADB\), отсюда \(\angle A = \angle B\). Таким образом, треугольник \(\triangle AMD\) равнобедренный, значит \(MA = MD\). Поскольку \(AB = CD\), то \(MC = MB\).
Таким образом, в обоих случаях доказано, что \(MA = MD\) и \(MC = MB\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.