ГДЗ по Геометрии 9 класс Номер 879 Атанасян — Подробные Ответы

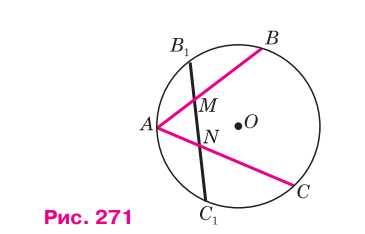
Точки \( B_1 \) и \( C_1 \) — середины дуг \( AB \) и \( AC \) (рис. 271). Докажите, что \( AM = AN \).  

Дано: Окружность \( (O; R) \). Углы \( \angle AB_1 = \angle B_1B = \frac{1}{2} \angle AB \), \( \angle AC_1 = \angle C_1C = \frac{1}{2} \angle AC \). Точки пересечения \( AB \cap B_1C_1 = M \), \( AC \cap BC = N \). Необходимо доказать, что \( AM = AN \).

Рассмотрим доказательство:

1. Углы \( \angle AB_1 = \angle B_1B = \frac{1}{2} \angle AB \). Следовательно, \( \angle B_1AB = \angle B_1BA = \angle B_1C_1A \).

2. Углы \( \angle AC_1 = \angle C_1C = \frac{1}{2} \angle AC \). Следовательно, \( \angle C_1AC = \angle C_1CA = \angle C_1B_1A \).

3. Из этого следует, что \( \angle AB_1M = \angle C_1AN \) и \( \angle B_1AM = \angle AC_1N \). Значит, \( \angle AMB_1 = \angle ANC_1 \).

4. Угол \( \angle AMN = 180^\circ — \angle AMB_1 — \angle ANM = 180^\circ — \angle ANC_1 \). Следовательно, \( \angle AMN = \angle ANM \), а значит, треугольник \( \triangle AMN \) равнобедренный. Отсюда \( AM = AN \), что и требовалось доказать.

Дано: окружность \((O; R)\), углы \(\angle AB_1 = \angle B_1B = \frac{1}{2} \angle AB\), \(\angle AC_1 = \angle C_1C = \frac{1}{2} \angle AC\). Точки пересечения \(AB \cap B_1C_1 = M\), \(AC \cap BC = N\). Требуется доказать, что \(AM = AN\).

Рассмотрим решение.

1. По условию углы \(\angle AB_1 = \angle B_1B = \frac{1}{2} \angle AB\). Это означает, что дуга \(AB_1\) равна дуге \(B_1B\), а следовательно, дуга \(AB_1\) также равна дуге \(B_1C_1\). Из этого следует, что \(\angle B_1AB = \angle B_1BA = \angle B_1C_1A\). Таким образом, треугольник \(\triangle AB_1C_1\) имеет равные углы при вершинах \(B_1\) и \(A\).

2. Аналогично, по условию углы \(\angle AC_1 = \angle C_1C = \frac{1}{2} \angle AC\). Это означает, что дуга \(AC_1\) равна дуге \(C_1C\), а следовательно, дуга \(AC_1\) также равна дуге \(C_1B_1\). Из этого следует, что \(\angle C_1AC = \angle C_1CA = \angle C_1B_1A\). Таким образом, треугольник \(\triangle AC_1B_1\) имеет равные углы при вершинах \(C_1\) и \(A\).

3. Рассмотрим точку \(M\) — точку пересечения \(AB\) и \(B_1C_1\). Углы \(\angle AB_1M\) и \(\angle C_1AN\) равны, так как вершины \(M\) и \(N\) находятся на одной и той же дуге окружности, а дуги \(AB_1\) и \(C_1A\) равны. Аналогично, углы \(\angle B_1AM\) и \(\angle AC_1N\) равны, так как вершины \(M\) и \(N\) находятся на одной и той же дуге окружности, а дуги \(B_1A\) и \(AC_1\) равны.

4. Из равенства углов \(\angle AB_1M = \angle C_1AN\) и \(\angle B_1AM = \angle AC_1N\) следует, что углы \(\angle AMB_1\) и \(\angle ANC_1\) равны. Это равенство углов означает, что треугольники \(\triangle AMB_1\) и \(\triangle ANC_1\) подобны.

5. Рассмотрим угол \(\angle AMN\). Этот угол равен \(180^\circ — \angle AMB_1 — \angle ANM\). Поскольку \(\angle AMB_1 = \angle ANC_1\), то \(\angle AMN = \angle ANM\). Таким образом, треугольник \(\triangle AMN\) равнобедренный.

6. В равнобедренном треугольнике стороны, прилежащие к равным углам, равны. Следовательно, \(AM = AN\).

Что и требовалось доказать.