ГДЗ по Геометрии 9 класс Номер 878 Атанасян — Подробные Ответы

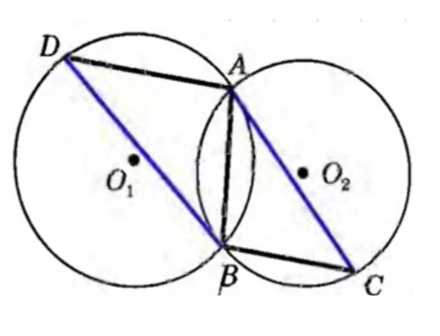
Прямая \( AC \) — касательная к окружности с центром \( O_1 \), а прямая \( BD \) — касательная к окружности с центром \( O_2 \) (рис. 270). Докажите, что:  

а) \( AD \parallel BC \);  

б) \( AB^2 = AD \cdot BC \);  

в) \( \frac{BD^2}{AC^2} = \frac{AD}{BC} \).  

Дано: точки \(O_1\) и \(O_2\) — центры окружностей радиусов \(r_1\) и \(r_2\), которые касаются друг друга в точке \(M\). \(O_1A \perp AC\), \(O_2B \perp BD\), \(AC\) и \(BD\) — касательные.

Доказать:
а) \(AD \parallel BC\);
б) \(AB^2 = AD \cdot BC\);
в) \(\frac{BD^2}{AC^2} = \frac{AD}{BC}\).

Рассмотрим доказательство.

а) Рассмотрим углы между хордами и касательными:
\[
\angle CAB = \frac{1}{2} \angle AB(O_1) = \angle ADB, \quad \angle DBA = \frac{1}{2} \angle AB(O_2) = \angle BCA.
\]
Следовательно, треугольники \(\triangle DAB\) и \(\triangle ABC\) подобны по двум углам. Из подобия треугольников следует, что \(\angle DAB = \angle ABC\). Так как накрест лежащие углы равны, то \(AD \parallel BC\), что и требовалось доказать.

б) Из подобия треугольников \(\triangle DAB\) и \(\triangle ABC\) следует пропорциональность сторон:
\[
\frac{AB}{AD} = \frac{BC}{AB}.
\]
Умножая обе части пропорции на \(AB\), получаем:
\[
AB^2 = AD \cdot BC,
\]
что и требовалось доказать.

в) Из подобия треугольников \(\triangle DAB\) и \(\triangle ABC\) следует:
\[
\frac{BD}{AD} = \frac{AC}{AB}.
\]
Возводя обе части пропорции в квадрат, получаем:
\[
\frac{BD^2}{AD^2} = \frac{AC^2}{AB^2}.
\]
Подставляя выражение из пункта б (\(AB^2 = AD \cdot BC\)), получаем:
\[
\frac{BD^2}{AC^2} = \frac{AD}{BC},
\]
что и требовалось доказать.

Дано: \(O_1\) и \(O_2\) — центры окружностей радиусов \(r_1\) и \(r_2\), которые касаются друг друга. \(O_1A \perp AC\), \(O_2B \perp BD\), \(AC\) и \(BD\) — касательные. Требуется доказать:

а) \(AD \parallel BC\);
б) \(AB^2 = AD \cdot BC\);
в) \(\frac{BD^2}{AC^2} = \frac{AD}{BC}\).

Рассмотрим доказательство.

а) Рассмотрим углы между хордами и касательными. Углы между касательной \(AC\) и хордой \(AB\) окружности с центром \(O_1\) равны половине угла дуги, на которую опирается хорда \(AB\). Аналогично углы между касательной \(BD\) и хордой \(AB\) окружности с центром \(O_2\) также равны половине угла дуги, на которую опирается хорда \(AB\):
\[
\angle CAB = \frac{1}{2} \angle AB(O_1), \quad \angle DBA = \frac{1}{2} \angle AB(O_2).
\]

Так как угол \(\angle CAB = \angle DBA\), то треугольники \(\triangle DAB\) и \(\triangle ABC\) подобны по двум углам. Из подобия треугольников следует, что \(\angle DAB = \angle ABC\). Эти углы являются накрест лежащими, а значит, прямые \(AD\) и \(BC\) параллельны:
\[
AD \parallel BC.
\]
Таким образом, пункт а доказан.

б) Из подобия треугольников \(\triangle DAB\) и \(\triangle ABC\) следует пропорциональность сторон:
\[
\frac{AB}{AD} = \frac{BC}{AB}.
\]

Умножая обе части пропорции на \(AB\), получаем:
\[
AB^2 = AD \cdot BC.
\]
Таким образом, пункт б доказан.

в) Из подобия треугольников \(\triangle DAB\) и \(\triangle ABC\) также следует пропорциональность сторон:
\[
\frac{BD}{AD} = \frac{AC}{AB}.
\]

Возводя обе части пропорции в квадрат, получаем:
\[
\frac{BD^2}{AD^2} = \frac{AC^2}{AB^2}.
\]

Подставляя выражение из пункта б (\(AB^2 = AD \cdot BC\)), получаем:
\[
\frac{BD^2}{AC^2} = \frac{AD}{BC}.
\]
Таким образом, пункт в доказан.

Вывод: все три пункта доказаны.