ГДЗ по Геометрии 9 класс Номер 876 Атанасян — Подробные Ответы

Постройте ромб, площадь которого равна площади данного квадрата, если известно, что отношение диагоналей этого ромба равно отношению данных отрезков.

Краткое решение задачи по построению ромба \(ABCD\):

1. Дано: \(MNPQ\) — квадрат, диагонали \(AC : BD = m : n\), площади \(S_{ABCD} = S_{MNPQ}\). Необходимо построить ромб \(ABCD\).

2. Уравнение для площади ромба:
\(
S_{ABCD} = \frac{1}{2} AC \cdot BD = \frac{1}{2} MQ \cdot PN
\)
Это означает, что \(AC \cdot BD = MQ \cdot PN\).

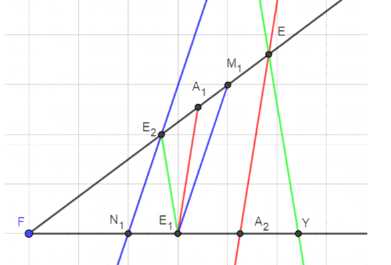
3. Построение произведения \(MQ\) и \(PN\) осуществляется через единичный отрезок \(e\).
Произведение \(m \cdot n\):
\(
FM_1 = m, \quad FN_1 = n, \quad FE_2 = m \cdot n
\)

4. Соотношение:
\(
\frac{FE}{FE_2} = FY = y
\)
Квадратный корень из \(y\):
\(
A_2Y = \sqrt{FY}
\)

5. Построение произведений:
\(
AN \cdot A_2Y, \quad AM \cdot A_2Y
\)
Таким образом:
\(
BD = A_2D, \quad AC = A_2C
\)

6. Построение ромба с данными диагоналями \(AC\) и \(BD\) завершается через построение окружности, где диагонали пересекаются под прямым углом.

Дано: \(MNPQ\) — квадрат, диагонали которого пересекаются в одной точке. Заданы отношения диагоналей ромба \(AC : BD = m : n\), а также площади \(S_{ABCD} = S_{MNPQ}\). Требуется построить ромб \(ABCD\).

1. Выразим площадь ромба \(S_{ABCD}\):
Формула площади ромба через диагонали:
\(
S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD
\)
Площадь квадрата \(S_{MNPQ}\):
\(
S_{MNPQ} = \frac{1}{2} \cdot MQ \cdot PN
\)
Так как \(S_{ABCD} = S_{MNPQ}\), то:
\(
\frac{1}{2} \cdot AC \cdot BD = \frac{1}{2} \cdot MQ \cdot PN
\)
Следовательно:
\(
AC \cdot BD = MQ \cdot PN
\)

2. Построим произведение \(MQ \cdot PN\) при единичном отрезке \(e\).
Пусть \(FE_1 = e\) — единичный отрезок. Тогда:
\(
FM_1 = m, \quad FN_1 = n, \quad FE_2 = m \cdot n
\)
Таким образом, отрезок \(FE_2\) представляет собой произведение \(m \cdot n\).

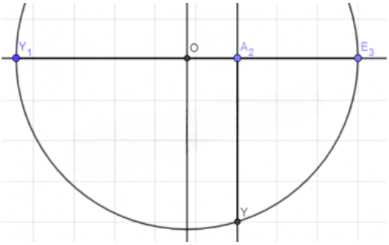
3. Найдем соотношение:
\(
\frac{FE}{FE_2} = FY = y
\)
Это соотношение позволяет определить отношение между длинами отрезков.

4. Найдем квадратный корень из \(y\):
Отрезок \(A_2Y\) равен квадратному корню из \(FY\):
\(
A_2Y = \sqrt{FY}
\)

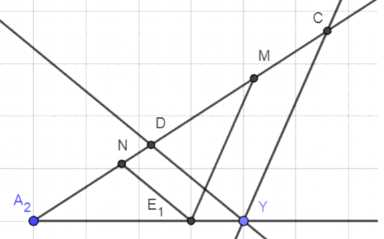
5. Построим произведения \(AN \cdot A_2Y\) и \(AM \cdot A_2Y\):
Используем отрезки \(AN\) и \(AM\) для построения диагоналей ромба. Таким образом:
\(
BD = A_2D, \quad AC = A_2C
\)

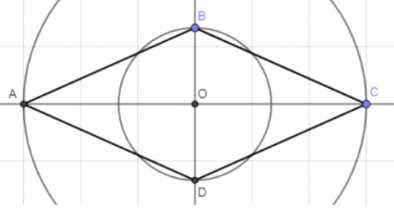
6. Построение ромба завершается следующим образом:
Диагонали ромба \(AC\) и \(BD\) пересекаются под прямым углом. Для построения ромба проводим окружность, в которой данные диагонали являются диаметрами. Вершины ромба \(A\), \(B\), \(C\), \(D\) располагаются на пересечении окружности с прямыми, проходящими через диагонали.

Таким образом, ромб \(ABCD\) с заданными диагоналями \(AC\) и \(BD\), а также равной площади \(S_{MNPQ}\), построен.