
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 875 Атанасян — Подробные Ответы
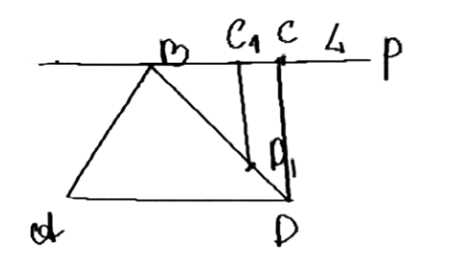
Постройте трапецию по боковой стороне, большему основанию, углу между ними и отношению двух других сторон.
Для построения трапеции \(ABCD\) выполняем следующие шаги:
1. На сторонах угла \(A\) откладываем отрезки \(AD = a\) и \(AB = b\). Эти отрезки соответствуют основанию \(a\) и боковой стороне \(b\).
2. Строим отрезок \(BD\), который является диагональю трапеции. Диагональ соединяет вершины \(B\) и \(D\).
3. Проводим прямую, параллельную \(AD\), и откладываем на ней отрезок \(BC_1\), равный \(m\). Здесь \(m\) — заданное значение.
4. Строим окружность с центром в точке \(C_1\) и радиусом \(n\). На пересечении этой окружности с отрезком \(BD\) отмечаем точку \(D_1\).
5. Через точку \(D\) проводим прямую, параллельную \(C_1D_1\). На пересечении этой прямой с прямой \(BC_1\) отмечаем точку \(C\).
Трапеция \(ABCD\) построена.
Для построения трапеции \(ABCD\) с заданными параметрами \(a\) (основание), \(b\) (боковая сторона), углом \(\angle A\), соотношением двух сторон \(n\), и длиной \(m\) выполняем следующие шаги:
1. На сторонах угла \(A\) откладываем отрезки \(AD = a\) и \(AB = b\). Для этого используем транспортир для точного построения угла \(\angle A\). Отрезок \(AD\) откладывается вдоль одной стороны угла, а \(AB\) вдоль другой стороны угла.
2. Строим отрезок \(BD\), который является диагональю трапеции. Диагональ соединяет вершины \(B\) и \(D\), её длина и направление определяются как соединение точек \(B\) и \(D\), которые уже построены.
3. Проводим прямую, параллельную \(AD\), и откладываем на ней отрезок \(BC_1\), равный \(m\). Для этого используем линейку и чертим прямую, параллельную \(AD\), и на этой прямой отмечаем длину \(m\), начиная от точки \(B\).
4. Строим окружность с центром в точке \(C_1\) и радиусом \(n\). Для этого используем циркуль, устанавливая его центр в точке \(C_1\) и радиус равным \(n\). Окружность пересекает отрезок \(BD\) в точке \(D_1\).
5. Через точку \(D\) проводим прямую, параллельную \(C_1D_1\). Для этого используем линейку и чертим прямую через точку \(D\), которая параллельна отрезку \(C_1D_1\). На пересечении этой прямой с прямой \(BC_1\) отмечаем точку \(C\).
Трапеция \(ABCD\) построена. Её вершины \(A\), \(B\), \(C\), \(D\) определены, а стороны соответствуют заданным параметрам.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!