
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 871 Атанасян — Подробные Ответы
Постройте равнобедренный треугольник по углу между боковыми сторонами и сумме основания и высоты, проведённой к основанию.
Дано: угол \( \beta \), отрезок \( a \). Построить треугольник \( \triangle ABC \), для которого \(\angle B = \beta\), \(AB = BC\), \(BH\) — высота, \(AC + BH = a\).
Решение:
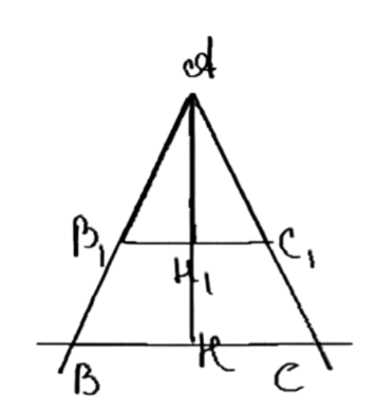
1. Построим угол \( \angle I = \beta \) и его биссектрису \( BB_1 \).
2. На произвольном расстоянии от вершины \( B \) строим перпендикуляр к биссектрисе и отмечаем точки пересечения \( A_1 \) и \( C_1 \) со сторонами угла.
3. Из вершины \( B \), под произвольным острым углом вне угла \( \beta \), проводим луч и откладываем на нем отрезок \( BR = a \). На этом же луче откладываем \( BR_1 = A_1C_1 + BH_1 \), где \( BH_1 \) — высота.
4. Проводим прямую \( H_1R_1 \) и параллельную ей прямую \( HR \). Точка \( H \) находится как пересечение \( HR \) и биссектрисы \( BB_1 \).
5. Через найденную точку \( H \) строим перпендикуляр к биссектрисе \( BB_1 \), отмечаем точки пересечения \( A \) и \( C \) со сторонами угла \( \beta \). Треугольник \( \triangle ABC \) — искомый.
Анализ:
Задача имеет решение для любого неразвернутого угла \( \beta < 180^\circ \) и \( a > 0 \).
Дано: угол \( \beta \), отрезок \( a \). Требуется построить треугольник \( \triangle ABC \), для которого выполняются условия: \( \angle B = \beta \), \( AB = BC \), \( BH \) — высота, \( AC + BH = a \).
Решение:
1. Построим угол \( \angle I = \beta \) с вершиной в точке \( B \). Для этого проведем две стороны угла, обозначим их как \( BA \) и \( BC \). Проведем биссектрису угла \( \beta \), обозначим ее как \( BB_1 \).
2. Выберем произвольное расстояние от вершины \( B \) и проведем перпендикуляр к биссектрисе \( BB_1 \). Этот перпендикуляр пересечет стороны угла \( \beta \) в двух точках. Обозначим точки пересечения как \( A_1 \) и \( C_1 \).
3. Из вершины \( B \) проводим луч под произвольным острым углом вне угла \( \beta \). На этом луче откладываем отрезок \( BR = a \). Затем на том же луче откладываем отрезок \( BR_1 = A_1C_1 + BH_1 \), где \( BH_1 \) — высота, опущенная из точки \( B \) на сторону \( AC \).
4. Через точки \( H_1 \) и \( R_1 \), которые получены на предыдущем шаге, проводим прямую \( H_1R_1 \). Затем строим прямую \( HR \), которая параллельна \( H_1R_1 \). Точка \( H \) находится как пересечение \( HR \) и биссектрисы \( BB_1 \).
5. Через точку \( H \), найденную на предыдущем шаге, проводим перпендикуляр к биссектрисе \( BB_1 \). Этот перпендикуляр пересечет стороны угла \( \beta \) в двух точках. Обозначим точки пересечения как \( A \) и \( C \).
6. Треугольник \( \triangle ABC \) является искомым. Проверим выполнение условий задачи: \( \angle B = \beta \), \( AB = BC \), \( BH \) — высота, и \( AC + BH = a \). Все условия выполнены.
Анализ:
Задача имеет решение для любого неразвернутого угла \( \beta < 180^\circ \) и положительного отрезка \( a > 0 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!