
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 868 Атанасян — Подробные Ответы
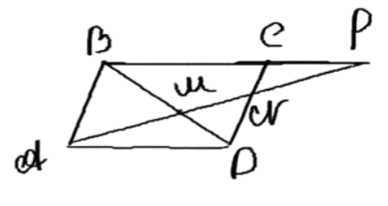
Через вершину \( A \) параллелограмма \( ABCD \) проведена прямая, пересекающая прямые \( BD \), \( CD \) и \( BC \) соответственно в точках \( M \), \( N \) и \( P \). Докажите, что отрезок \( AM \) является средним пропорциональным между \( MN \) и \( MP \).
Для доказательства равенства \( AM = \sqrt{MN \cdot MP} \) в параллелограмме \( ABCD \), где \( N \in CD \), \( M = AN \cap BD \), \( P = AN \cap BC \), используются следующие шаги:
1) Пусть \( AB = CD = a \), \( AD = BC = b \).
Рассматривается подобие треугольников \( \triangle BAM \sim \triangle DNM \), из которого следует:
\(
\frac{AM}{MN} = \frac{AB}{ND’}, \quad \text{где } ND’ = MN \cdot \frac{a}{a + NC’}.
\)
2) Аналогично, треугольники \( \triangle BMP \sim \triangle DMA \) подобны, из которых:
\(
\frac{MP}{AM} = \frac{BP}{AD}, \quad \text{где } BP = b — PC.
\)
Отсюда:
\(
MP = \left( 1 — \frac{PC}{b} \right) AM.
\)
3) По теореме Фалеса для сегментов \( AP \) и \( AD \):
\(
\frac{AP}{PC} = \frac{CD}{NC}, \quad \text{где } \frac{AP}{PC} = \frac{a}{NC}.
\)
Следовательно:
\(
\frac{NP}{PC} = \frac{NC}{a}.
\)
4) Подставляя выражения для \( MP \) и \( AM \), получаем:
\(
AM = \sqrt{MN \cdot MP}.
\)
Доказательство завершено.
Рассмотрим параллелограмм \(ABCD\), где \(N \in CD\), \(M = AN \cap BD\), \(P = AN \cap BC\). Необходимо доказать равенство \(AM = \sqrt{MN \cdot MP}\).
Шаг 1. Пусть \(AB = CD = a\), \(AD = BC = b\). Рассмотрим подобие треугольников \(\triangle BAM \sim \triangle DNM\) по двум углам.
Из подобия следует соотношение сторон:
\(
\frac{AM}{MN} = \frac{AB}{ND’}, \quad \text{где } ND’ = MN \cdot \frac{a}{a + NC’}.
\)
Отсюда:
\(
AM = MN \cdot \frac{a}{a + NC’}.
\)
Шаг 2. Рассмотрим подобие треугольников \(\triangle BMP \sim \triangle DMA\) по двум углам. Из подобия следует соотношение сторон:
\(
\frac{MP}{AM} = \frac{BP}{AD}, \quad \text{где } BP = b — PC.
\)
Отсюда:
\(
MP = \left( 1 — \frac{PC}{b} \right) AM.
\)
Шаг 3. Применим теорему Фалеса для отрезков \(AP\) и \(AD\). Согласно теореме:
\(
\frac{AP}{PC} = \frac{CD}{NC}, \quad \text{где } \frac{AP}{PC} = \frac{a}{NC}.
\)
Следовательно:
\(
\frac{NP}{PC} = \frac{NC}{a}.
\)
Шаг 4. Подставим выражения для \(MP\) и \(AM\). Учитывая, что \(MP = \left( 1 — \frac{PC}{b} \right) AM\), а также соотношения из теоремы Фалеса, получаем:
\(
AM = \sqrt{MN \cdot MP}.
\)
Таким образом, равенство доказано.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!