
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 867 Атанасян — Подробные Ответы
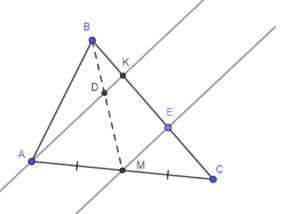
В треугольнике \( ABC \) прямая, проходящая через вершину \( A \) и делящая медиану \( BM \) в отношении \( 1 : 2 \), считая от вершины, пересекает сторону \( BC \) в точке \( K \). Найдите отношение площадей треугольников \( ABK \) и \( ABC \).
Дано: треугольник \( \triangle ABC \), медиана \( BM \), точка \( D \) на медиане \( BM \), где \( BD = \frac{1}{3}BM \), и точка \( K = AD \cap BC \). Найти отношение площадей \( S_{ABK} \) и \( S_{ABC} \).
Решение:
1) Проведем прямую \( ME \parallel AK \), где \( E \in BC \). Для \( \triangle AKC \) прямая \( ME \) является средней линией, так как \( ME \parallel AK \) и \( AM = MC \). Следовательно, \( KE = EC \).
2) По теореме Фалеса для \( \triangle MBC \):
\(
\frac{BD}{DM} = \frac{BK}{KE} = \frac{1}{2},
\)
откуда \( BK : KE : EC = 1 : 2 : 2 \). Таким образом, \( BK = \frac{1}{5}BC \).
3) Треугольник \( \triangle ABK \) имеет в 5 раз меньшее основание (\( BK = \frac{1}{5}BC \)) и ту же высоту, что и \( \triangle ABC \). Следовательно:
\(
\frac{S_{ABK}}{S_{ABC}} = \frac{1}{5}.
\)
Ответ: \( \frac{1}{5} \).
Дано: треугольник \( \triangle ABC \), медиана \( BM \), точка \( D \) на медиане \( BM \), где \( BD = \frac{1}{3}BM \), и точка \( K = AD \cap BC \). Найти отношение площадей \( S_{ABK} \) и \( S_{ABC} \).
Решение:
1. Рассмотрим треугольник \( \triangle ABC \), где медиана \( BM \) делит сторону \( AC \) пополам, то есть \( AM = MC \). Точка \( D \) находится на медиане \( BM \) так, что \( BD = \frac{1}{3}BM \), а \( DM = \frac{2}{3}BM \).
2. Проведем прямую \( ME \parallel AK \), где \( E \in BC \). Для треугольника \( \triangle AKC \) прямая \( ME \) является средней линией, так как \( ME \parallel AK \) и \( AM = MC \). По свойству средней линии треугольника, \( KE = EC \).
3. Применим теорему Фалеса для треугольника \( \triangle MBC \). Согласно теореме:
\(
\frac{BD}{DM} = \frac{BK}{KE}.
\)
Подставим значения:
\(
\frac{BD}{DM} = \frac{1}{2}.
\)
Таким образом, \( BK : KE : EC = 1 : 2 : 2 \).
4. Учитывая, что \( BK + KE + EC = BC \), получаем:
\(
BK = \frac{1}{5}BC, \quad KE = \frac{2}{5}BC, \quad EC = \frac{2}{5}BC.
\)
5. Рассмотрим треугольник \( \triangle ABK \). Его основание \( BK \) равно \( \frac{1}{5}BC \), а высота совпадает с высотой треугольника \( \triangle ABC \), так как вершина \( A \) общая для обоих треугольников.
6. Площадь треугольника пропорциональна произведению основания на высоту. Следовательно, отношение площадей \( \triangle ABK \) и \( \triangle ABC \) равно отношению оснований:
\(
\frac{S_{ABK}}{S_{ABC}} = \frac{BK}{BC}.
\)
Подставим значение \( BK = \frac{1}{5}BC \):
\(
\frac{S_{ABK}}{S_{ABC}} = \frac{1}{5}.
\)
Ответ: \( \frac{1}{5} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!