
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 866 Атанасян — Подробные Ответы
Стороны треугольника \( EFG \) соответственно равны медианам треугольника \( ABC \). Докажите, что
\(
\frac{S_{EFG}}{S_{ABC}} = \frac{3}{4}.
\)
Рассмотрим доказательство:
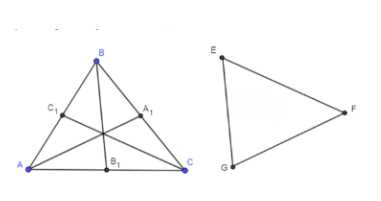
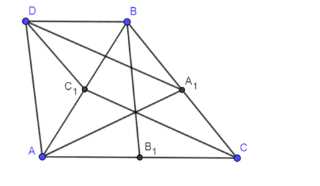
1. Проведем \( AD \parallel BB_1 \) и \( BD \parallel AC \). Четырехугольник \( ADBB_1 \) является параллелограммом, так как \( AD = BB_1 \), а \( BD = AB_1 \). Следовательно, \( AC = A_1C_1 \). Точка \( C_1 \) делит диагональ \( AB \) пополам, а значит, делит и диагональ \( B_1D \) пополам: \( C_1D = \frac{1}{2}B_1D = \frac{1}{2}BC \).
Четырехугольник \( BDB_1C \) также является параллелограммом, так как \( BD \parallel AC \), а \( BD = B_1C = \frac{1}{2}AC \). Аналогично, четырехугольник \( DC_1CA_1 \) — параллелограмм, так как \( DC_1 \parallel A_1C \) и \( DC_1 = A_1C \). Значит, в треугольнике \( \triangle ADA_1 \) выполняется: \( AD = BB_1 \), \( DA_1 = CC_1 \), следовательно, \( \triangle ADA_1 \) — искомый треугольник, построенный на медианах треугольника \( \triangle ABC \).
2. Найдем площадь \( \triangle ADA_1 \). Площадь \( \triangle ADA_1 \) равна сумме площадей:
\( S_{ADA_1} = S_{AC_1D} + S_{AC_1A_1} + S_{A_1C_1D} \).
Площадь \( \triangle ABD \) равна половине площади \( \triangle ABC \), так как основание \( BD \) вдвое меньше основания \( AC \), а высота одинаковая. Площадь \( \triangle ABA_1 \) также равна половине площади \( \triangle ABC \), так как основание \( AB_1 \) вдвое меньше основания \( AB \), а высота одинаковая. Площадь \( \triangle A_1C_1B \) составляет четверть площади \( \triangle ABC \), так как и основание, и высота уменьшены вдвое.
Таким образом:
\( S_{ADA_1} = \frac{1}{2}S_{ABC} + \frac{1}{2}S_{ABC} + \frac{1}{4}S_{ABC} = \frac{3}{4}S_{ABC} \).
3. По построению треугольник \( \triangle ADA_1 \) равен треугольнику \( \triangle EFG \), следовательно:
\( S_{EFG} = \frac{3}{4}S_{ABC} \).
Доказательство завершено.
Рассмотрим задачу подробно.
Дано: треугольник \( \triangle ABC \), медианы \( AA_1, BB_1, CC_1 \). Четырехугольник \( \triangle EFG \) построен на медианах треугольника \( \triangle ABC \). Требуется доказать, что площадь \( S_{EFG} = \frac{3}{4} S_{ABC} \).
1. Для построения проведем \( AD \parallel BB_1 \) и \( BD \parallel AC \). Четырехугольник \( ADBB_1 \) является параллелограммом, так как \( AD = BB_1 \) и \( BD = AB_1 \). Следовательно, \( AC = A_1C_1 \). Точка \( C_1 \) делит диагональ \( AB \) пополам, а значит, делит и диагональ \( B_1D \) пополам:
\( C_1D = \frac{1}{2}B_1D = \frac{1}{2}BC. \)
Четырехугольник \( BDB_1C \) также является параллелограммом, так как \( BD \parallel AC \) и \( BD = B_1C = \frac{1}{2}AC \). Аналогично, четырехугольник \( DC_1CA_1 \) — параллелограмм, так как \( DC_1 \parallel A_1C \) и \( DC_1 = A_1C \). Значит, в треугольнике \( \triangle ADA_1 \) выполняется:
\( AD = BB_1, \quad DA_1 = CC_1, \)
следовательно, \( \triangle ADA_1 \) — искомый треугольник, построенный на медианах треугольника \( \triangle ABC \).
2. Найдем площадь \( \triangle ADA_1 \). Площадь \( \triangle ADA_1 \) равна сумме площадей:
\( S_{ADA_1} = S_{AC_1D} + S_{AC_1A_1} + S_{A_1C_1D}. \)
Площадь \( \triangle ABD \) равна половине площади \( \triangle ABC \), так как основание \( BD \) вдвое меньше основания \( AC \), а высота одинаковая:
\( S_{ABD} = \frac{1}{2}S_{ABC}. \)
Площадь \( \triangle ABA_1 \) также равна половине площади \( \triangle ABC \), так как основание \( AB_1 \) вдвое меньше основания \( AB \), а высота одинаковая:
\( S_{ABA_1} = \frac{1}{2}S_{ABC}. \)
Площадь \( \triangle A_1C_1B \) составляет четверть площади \( \triangle ABC \), так как и основание, и высота уменьшены вдвое:
\( S_{A_1C_1B} = \frac{1}{4}S_{ABC}. \)
Таким образом:
\(
S_{ADA_1} = S_{AC_1D} + S_{AC_1A_1} + S_{A_1C_1D} = \frac{1}{2}S_{ABC} + \frac{1}{2}S_{ABC} + \frac{1}{4}S_{ABC} = \frac{3}{4}S_{ABC}.
\)
3. По построению треугольник \( \triangle ADA_1 \) равен треугольнику \( \triangle EFG \), следовательно:
\( S_{EFG} = \frac{3}{4}S_{ABC}. \)
Доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!