
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 865 Атанасян — Подробные Ответы
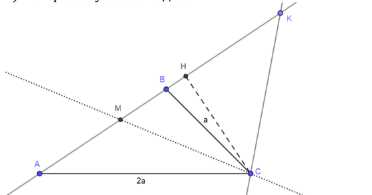
В треугольнике \( ABC \), сторона \( AC \) которого в два раза больше стороны \( BC \), проведены биссектриса \( CM \) и биссектриса внешнего угла при вершине \( C \), пересекающая прямую \( AB \) в точке \( K \). Докажите, что
\(
S_{BCM} = \frac{1}{2} S_{ACM} = \frac{1}{3} S_{ABC} = \frac{1}{5} S_{CMK}.
\)
Рассмотрим треугольник \( \triangle ABC \), где \( AC = 2BC \), \( CM \) — биссектриса, \( CK = 1 \cdot CM \), точка \( K \) лежит на \( AB \). Требуется доказать, что:
1. \( S_{BCM} = \frac{1}{2} S_{ACM} \),
2. \( S_{BCM} = \frac{1}{4} S_{CMK} \).
Пусть \( BC = a \), тогда \( AC = 2a \). У всех рассматриваемых треугольников одна высота \( CH \), проведённая из вершины \( C \) на \( AB \). Площади треугольников пропорциональны длинам их оснований.
По теореме о биссектрисе:
\(
\frac{AM}{AC} = \frac{BM}{BC}, \quad \frac{AM}{2a} = \frac{BM}{a}.
\)
Отсюда:
\(
BM = \frac{1}{2} AM, \quad AM = \frac{2}{3} AB, \quad BM = \frac{1}{3} AB.
\)
Следовательно:
\(
S_{BCM} = \frac{1}{3} S_{ABC}, \quad S_{ACM} = \frac{2}{3} S_{ABC}.
\)
Таким образом:
\(
S_{BCM} = \frac{1}{2} S_{ACM}.
\)
Теперь рассмотрим точку \( K \), которая делит биссектрису \( CM \) в отношении \( CK : KM = 1 : 1 \).
По теореме о биссектрисе внешнего угла:
\(
\frac{BK}{AK} = \frac{BC}{AC}, \quad \frac{BK}{AK} = \frac{a}{2a} = \frac{1}{2}.
\)
Отсюда:
\(
BK = \frac{1}{3} AB, \quad KM = BM + BK = \frac{1}{3} AB + \frac{1}{3} AB = \frac{4}{3} BM.
\)
Следовательно:
\(
S_{CMK} = \frac{4}{3} S_{BCM}.
\)
И наконец:
\(
S_{BCM} = \frac{1}{4} S_{CMK}.
\)
Все равенства доказаны.
Рассмотрим задачу. Дано: треугольник \( \triangle ABC \), где \( AC = 2BC \), \( CM \) — биссектриса, \( CK = 1 \cdot CM \), точка \( K \) лежит на \( AB \). Требуется доказать:
1. \( S_{BCM} = \frac{1}{2} S_{ACM} \),
2. \( S_{BCM} = \frac{1}{4} S_{CMK} \).
Решение:
1. Пусть \( BC = a \), тогда \( AC = 2a \). У всех рассматриваемых треугольников одна высота \( CH \), проведённая из вершины \( C \) на \( AB \). Площади треугольников пропорциональны длинам их оснований. Это следует из формулы площади треугольника:
\(
S = \frac{1}{2} \cdot основание \cdot высота.
\)
2. По теореме о биссектрисе внутреннего угла (задача 535):
\(
\frac{AM}{AC} = \frac{BM}{BC}.
\)
Подставим \( AC = 2a \) и \( BC = a \):
\(
\frac{AM}{2a} = \frac{BM}{a}.
\)
Умножим обе части на \( 2a \):
\(
AM = 2BM.
\)
Кроме того, известно, что \( AB = AM + BM \). Подставим \( AM = 2BM \):
\(
AB = 2BM + BM = 3BM.
\)
Таким образом:
\(
BM = \frac{1}{3} AB, \quad AM = \frac{2}{3} AB.
\)
3. Найдём площади треугольников \( \triangle BCM \) и \( \triangle ACM \). Поскольку их высоты равны, площади пропорциональны основаниям \( BM \) и \( AM \):
\(
S_{BCM} = \frac{BM}{AB} \cdot S_{ABC}, \quad S_{ACM} = \frac{AM}{AB} \cdot S_{ABC}.
\)
Подставим значения \( BM \) и \( AM \):
\(
S_{BCM} = \frac{1}{3} S_{ABC}, \quad S_{ACM} = \frac{2}{3} S_{ABC}.
\)
Теперь вычислим отношение \( \frac{S_{BCM}}{S_{ACM}} \):
\(
\frac{S_{BCM}}{S_{ACM}} = \frac{\frac{1}{3} S_{ABC}}{\frac{2}{3} S_{ABC}} = \frac{1}{2}.
\)
Таким образом:
\(
S_{BCM} = \frac{1}{2} S_{ACM}.
\)
4. Рассмотрим точку \( K \), которая делит биссектрису \( CM \) в отношении \( CK : KM = 1 : 1 \). По теореме о биссектрисе внешнего угла (задача 619):
\(
\frac{BK}{AK} = \frac{BC}{AC}.
\)
Подставим \( BC = a \) и \( AC = 2a \):
\(
\frac{BK}{AK} = \frac{a}{2a} = \frac{1}{2}.
\)
Отсюда:
\(
BK = \frac{1}{3} AB, \quad AK = \frac{2}{3} AB.
\)
5. Найдём длину \( KM \). Поскольку \( KM = BM + BK \), подставим значения \( BM = \frac{1}{3} AB \) и \( BK = \frac{1}{3} AB \):
\(
KM = BM + BK = \frac{1}{3} AB + \frac{1}{3} AB = \frac{2}{3} AB.
\)
6. Найдём отношение площадей \( S_{BCM} \) и \( S_{CMK} \). Площади пропорциональны основаниям \( BM \) и \( KM \):
\(
\frac{S_{BCM}}{S_{CMK}} = \frac{BM}{KM}.
\)
Подставим значения \( BM \) и \( KM \):
\(
\frac{S_{BCM}}{S_{CMK}} = \frac{\frac{1}{3} AB}{\frac{2}{3} AB} = \frac{1}{2}.
\)
Таким образом:
\(
S_{BCM} = \frac{1}{4} S_{CMK}.
\)
Все равенства доказаны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!