
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 863 Атанасян — Подробные Ответы
Отрезки \( AA_1 \), \( BB_1 \) и \( CC_1 \) соединяют вершины треугольника \( ABC \) с внутренними точками противоположных сторон. Докажите, что середины этих отрезков не лежат на одной прямой.
Дано: \( \triangle ABC \), точки \( A_1 \in BC \), \( B_1 \in AC \), \( C_1 \in AB \).
Средние линии треугольника:
\( AD = DB, \ BE = EC, \ AF = FC \),
\( DE \parallel AC, \ EF \parallel AB, \ DF \parallel BC \).
Требуется доказать, что точки \( M, N, K \) не лежат на одной прямой.
Решение:
1. При перемещении точки \( A_1 \) вдоль стороны \( BC \), точка \( M \) будет перемещаться по средней линии \( DF \). Аналогично, точка \( N \) будет перемещаться по средней линии \( DE \), а точка \( K \) — по средней линии \( EF \).
2. Предположим, что точки \( M, N, K \) лежат на одной прямой. Тогда точки \( D, E, F \) также должны лежать на одной прямой.
3. Если точки \( D, E, F \) лежат на одной прямой, то точки \( A, B, C \) также лежат на одной прямой, что противоречит условию задачи, так как \( \triangle ABC \) — треугольник.
Следовательно, наше предположение неверно, и точки \( M, N, K \) не лежат на одной прямой.
Дано: \( \triangle ABC \), точки \( A_1 \in BC \), \( B_1 \in AC \), \( C_1 \in AB \).
Средние линии треугольника:
\( AD = DB, \ BE = EC, \ AF = FC \),
\( DE \parallel AC, \ EF \parallel AB, \ DF \parallel BC \).
Требуется доказать, что точки \( M, N, K \) не лежат на одной прямой.
Решение:
1. Построим все средние линии треугольника \( \triangle ABC \):
Средняя линия \( AD \) делит сторону \( BC \) на две равные части, то есть \( AD = DB \).
Средняя линия \( BE \) делит сторону \( AC \) на две равные части, то есть \( BE = EC \).
Средняя линия \( AF \) делит сторону \( AB \) на две равные части, то есть \( AF = FC \).
Кроме того, известно, что \( DE \parallel AC \), \( EF \parallel AB \), \( DF \parallel BC \).
2. Рассмотрим движение точки \( A_1 \) вдоль стороны \( BC \).
При перемещении точки \( A_1 \) точка \( M \), которая лежит на отрезке \( AA_1 \), будет перемещаться вдоль средней линии \( DF \). Аналогично, точка \( N \), которая лежит на отрезке \( BB_1 \), будет перемещаться вдоль средней линии \( DE \), а точка \( K \), которая лежит на отрезке \( CC_1 \), будет перемещаться вдоль средней линии \( EF \).
3. Предположим, что точки \( M, N, K \) лежат на одной прямой.
Если точки \( M, N, K \) лежат на одной прямой, то точки \( D, E, F \), которые являются вершинами треугольника, также должны лежать на одной прямой.
4. Если точки \( D, E, F \) лежат на одной прямой, то точки \( A, B, C \), которые являются вершинами исходного треугольника \( \triangle ABC \), также лежат на одной прямой.
Однако это противоречит условию задачи, так как \( \triangle ABC \) — треугольник, а треугольник не может быть образован, если его вершины лежат на одной прямой.
5. Следовательно, наше предположение о том, что точки \( M, N, K \) лежат на одной прямой, неверно.
Вывод: точки \( M, N, K \) не лежат на одной прямой.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


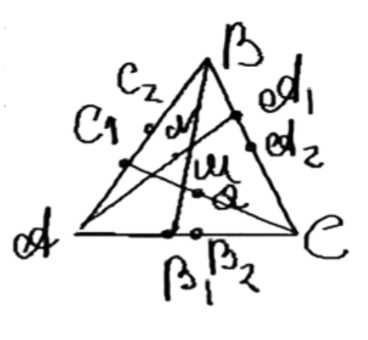

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!