ГДЗ по Геометрии 9 класс Номер 862 Атанасян — Подробные Ответы

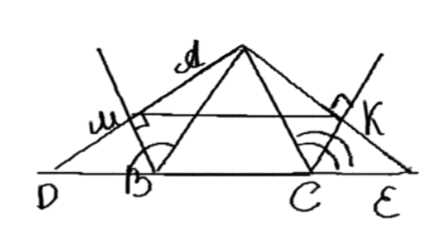
Из вершины \( A \) треугольника \( ABC \) проведены перпендикуляры \( AM \) и \( AK \) к биссектрисам внешних углов этого треугольника при вершинах \( B \) и \( C \). Докажите, что отрезок \( MK \) равен половине периметра треугольника \( ABC \).

Дано: ΔABC, OB и OC — биссектриссы внешних углов, O — точка пересечения OB и OC, AM = OB, AK = OC.
Требуется доказать: MK = (AB + BC + AC) / 2.

Решение:

1. Отметим точки пересечения: D = MK ∩ AB, E = MK ∩ AC, F = AM ∩ BC, G = AK ∩ BC.
2. В ΔFBA отрезок BM является одновременно биссектриссой и высотой. Следовательно, ΔFBA равнобедренный с основанием FA. Таким образом, FB = AB, FM = MA.
3. В ΔACG отрезок CK является одновременно биссектриссой и высотой. Следовательно, ΔACG равнобедренный с основанием AG. Таким образом, CG = AC, AK = KG.
4. FG = FB + BC + CG = AB + BC + AC.
5. Так как FM = MA и AK = KG, то MK является средней линией. Следовательно, MK = FG / 2 = (AB + BC + AC) / 2.

Ответ: MK = (AB + BC + AC) / 2.

Дано: треугольник \( \triangle ABC \), \( OB \) и \( OC \) — биссектриссы внешних углов, \( O \) — точка пересечения \( OB \) и \( OC \), \( AM = OB \), \( AK = OC \).
Требуется доказать, что \( MK = \frac{AB + BC + AC}{2} \).

Рассмотрим решение задачи:

1. Обозначим точки пересечения:
\( D = MK \cap AB \),
\( E = MK \cap AC \),
\( F = AM \cap BC \),
\( G = AK \cap BC \).

2. Рассмотрим треугольник \( \triangle FBA \):
В этом треугольнике отрезок \( BM \) является одновременно биссектриссой и высотой.
Следовательно, треугольник \( \triangle FBA \) равнобедренный с основанием \( FA \).
Из равнобедренности имеем:
\( FB = AB \),
\( FM = MA \).

3. Рассмотрим треугольник \( \triangle ACG \):
В этом треугольнике отрезок \( CK \) является одновременно биссектриссой и высотой.
Следовательно, треугольник \( \triangle ACG \) равнобедренный с основанием \( AG \).
Из равнобедренности имеем:
\( CG = AC \),
\( AK = KG \).

4. Теперь рассмотрим отрезок \( FG \):
\( FG = FB + BC + CG \).
Подставляя значения:
\( FG = AB + BC + AC \).

5. Так как \( FM = MA \) и \( AK = KG \), то \( MK \) является средней линией в трапеции \( FGMA \).
Следовательно:
\( MK = \frac{FG}{2} = \frac{AB + BC + AC}{2} \).

Таким образом, доказано, что \( MK = \frac{AB + BC + AC}{2} \).