ГДЗ по Геометрии 9 класс Номер 861 Атанасян — Подробные Ответы

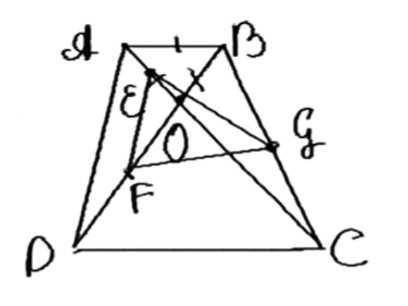
Диагонали трапеции \( ABCD \) пересекаются в точке \( O \). Треугольник \( ABO \), где \( AB \) — меньшее основание трапеции, равносторонний. Докажите, что треугольник, вершинами которого являются середины отрезков \( OA \), \( OD \) и \( BC \), равносторонний.

Дано: \( ABCD \) — трапеция, \( AB \parallel CD \), \( AB < CD \), \( O \) — точка пересечения диагоналей \( AC \) и \( BD \), \( \triangle AOB \) — равносторонний, \( M \in OA \), \( N \in BC \), \( K \in OD \), \( AM = MO \), \( BN = NC \), \( OK = KD \).
Доказать: \( \triangle MNK \) — равносторонний.

Решение:

1) Пусть \( OA = OB = AB = a \), \( CD = b \).
2) Проведем прямую \( KE \parallel CD \), где \( E \in OC \).
Так как \( KE \parallel CD \), то \( \angle AOB = \angle KOE \) (как вертикальные углы).
Следовательно, \( \triangle KOE \sim \triangle BOA \) (по двум углам).
\( \triangle KOE \) — равносторонний.
3) По построению \( KE \) — средняя линия \( \triangle DOC \), значит:
\[
KE = \frac{1}{2} CD = \frac{1}{2} b, \quad OK = OE = \frac{1}{2} b.
\]
4) Аналогично \( \triangle DOC \sim \triangle BOA \), значит \( \triangle DOC \) — равносторонний, \( OC = OD = CD = b \).
Тогда \( \triangle DOC \cong \triangle BOA \) (по двум сторонам и вертикальному углу).
5) \( NE \) — средняя линия \( \triangle BOC \), следовательно:
\[
NE = \frac{1}{2} OB = \frac{1}{2} a, \quad NE \perp OB, \quad \angle NEO = \angle BOA = 60^\circ.
\]
6) \( KO = KE = \frac{1}{2} b, \quad MO = EN = \frac{1}{2} a. \)
Углы:
\( \angle KOM = \angle KEN = 120^\circ \), следовательно \( \triangle KOM \cong \triangle KEN \).
Значит:
\[
KM = KN, \quad \angle MKO = \angle NKE.
\]
7) Угол \( \angle MKN = \angle KOE + \angle MKO — \angle NKE = 60^\circ. \)
8) Таким образом, \( \triangle MNK \) равнобедренный, \( KM = KN \), угол по вершине \( \angle MKN = 60^\circ \).
Значит, два угла при основании также равны \( 60^\circ \), и \( \triangle MNK \) — равносторонний.

Дано: \( ABCD \) — трапеция, \( AB \parallel CD \), \( AB < CD \), \( O \) — точка пересечения диагоналей \( AC \) и \( BD \), \( \triangle AOB \) — равносторонний, \( M \in OA \), \( N \in BC \), \( K \in OD \), \( AM = MO \), \( BN = NC \), \( OK = KD \).
Требуется доказать, что \( \triangle MNK \) — равносторонний.

Решение:

1. Пусть \( OA = OB = AB = a \), \( CD = b \).
Так как \( AB \parallel CD \), трапеция \( ABCD \) симметрична относительно оси, проходящей через точку \( O \).
Угол \( \angle AOB = 60^\circ \), так как \( \triangle AOB \) равносторонний.

2. Проведем прямую \( KE \parallel CD \), где \( E \in OC \).
Углы \( \angle AOB \) и \( \angle KOE \) равны как вертикальные.
Следовательно, \( \triangle KOE \sim \triangle BOA \) по двум углам.
Поскольку \( \triangle BOA \) равносторонний, то и \( \triangle KOE \) равносторонний.

3. По построению \( KE \) — средняя линия \( \triangle DOC \), значит:
\[
KE = \frac{1}{2} \cdot CD = \frac{1}{2} b, \quad OK = OE = \frac{1}{2} b.
\]

4. Аналогично, \( \triangle DOC \sim \triangle BOA \), так как они имеют равные углы и пропорциональные стороны.
Следовательно, \( \triangle DOC \) равносторонний, \( OC = OD = CD = b \).
Тогда \( \triangle DOC \cong \triangle BOA \) (по двум сторонам и вертикальному углу).

5. \( NE \) — средняя линия \( \triangle BOC \), следовательно:
\[
NE = \frac{1}{2} \cdot OB = \frac{1}{2} a, \quad NE \perp OB, \quad \angle NEO = \angle BOA = 60^\circ.
\]

6. Рассмотрим отрезки:
\[
KO = KE = \frac{1}{2} b, \quad MO = EN = \frac{1}{2} a.
\]
Углы:
\( \angle KOM = \angle KEN = 120^\circ \), следовательно \( \triangle KOM \cong \triangle KEN \) по стороне и углу.
Таким образом:
\[
KM = KN, \quad \angle MKO = \angle NKE.
\]

7. Угол \( \angle MKN \) можно найти как сумму углов:
\[
\angle MKN = \angle KOE + \angle MKO — \angle NKE = 60^\circ.
\]

8. Таким образом, \( \triangle MNK \) равнобедренный, \( KM = KN \), угол по вершине \( \angle MKN = 60^\circ \).
Значит, два угла при основании также равны \( 60^\circ \), и \( \triangle MNK \) — равносторонний.

Ответ: \( \triangle MNK \) — равносторонний.