
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 860 Атанасян — Подробные Ответы
Докажите, что если отрезок, соединяющий середины двух противоположных сторон выпуклого четырёхугольника, равен полусумме двух других сторон, то этот четырёхугольник — трапеция или параллелограмм.
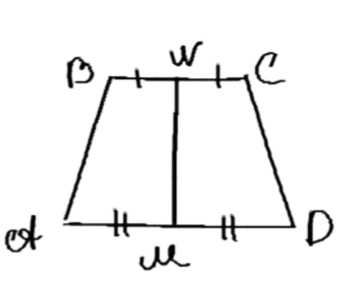
Дано: ABCD — выпуклый четырехугольник. \( M \in AB \), \( N \in CD \), \( AM = MB \), \( CN = ND \), \( MN = \frac{AB + BC}{2} \).
Доказать: ABCD — параллелограмм или трапеция.
Рассмотрим несколько возможных случаев.
1) Пусть стороны четырехугольника попарно не параллельны.
В этом случае \( MN \) — отрезок, соединяющий середины сторон \( AB \) и \( CD \). Согласно теореме о средней линии четырехугольника, выполняется неравенство:
\( MN < \frac{AB + BC}{2}. \)
Это противоречит условию задачи, так как по условию \( MN = \frac{AB + BC}{2} \). Следовательно, этот случай невозможен.
2) Пусть \( AD \parallel BC \), но \( AB \) не параллельно \( CD \).
В этом случае \( MN \) — средняя линия трапеции с основаниями \( AB \) и \( CD \). Для трапеции известно, что средняя линия равна полусумме оснований. Следовательно:
\( MN = \frac{AB + CD}{2}. \)
Однако по условию задачи \( MN = \frac{AB + BC}{2} \). Такое равенство возможно только в случае, если \( AB = CD \), то есть трапеция является равнобедренной.
3) Пусть \( AD \parallel BC \) и \( AB \parallel CD \).
В этом случае четырехугольник ABCD — параллелограмм. Для параллелограмма известно, что отрезок, соединяющий середины противоположных сторон, равен полусумме этих сторон. Следовательно:
\( MN = \frac{AB + BC}{2}. \)
Это равенство выполняется всегда, независимо от расположения сторон.
Таким образом, если выполняется условие \( MN = \frac{AB + BC}{2} \), то четырехугольник ABCD либо является параллелограммом, либо равнобедренной трапецией.
Ответ: ABCD — параллелограмм или равнобедренная трапеция.
Дано: ABCD — выпуклый четырехугольник. \( M \in AB \), \( N \in CD \), \( AM = MB \), \( CN = ND \), \( MN = \frac{AB + BC}{2} \).
Доказать: ABCD — параллелограмм или трапеция.
Рассмотрим несколько возможных случаев.
1) Пусть стороны четырехугольника попарно не параллельны.
В этом случае \( MN \) — отрезок, соединяющий середины сторон \( AB \) и \( CD \). Согласно теореме о средней линии четырехугольника, выполняется неравенство:
\( MN < \frac{AB + BC}{2}. \)
Это противоречит условию задачи, так как по условию \( MN = \frac{AB + BC}{2} \). Следовательно, этот случай невозможен.
2) Пусть \( AD \parallel BC \), но \( AB \) не параллельно \( CD \).
В этом случае \( MN \) — средняя линия трапеции с основаниями \( AB \) и \( CD \). Для трапеции известно, что средняя линия равна полусумме оснований. Следовательно:
\( MN = \frac{AB + CD}{2}. \)
Однако по условию задачи \( MN = \frac{AB + BC}{2} \). Такое равенство возможно только в случае, если \( AB = CD \), то есть трапеция является равнобедренной.
3) Пусть \( AD \parallel BC \) и \( AB \parallel CD \).
В этом случае четырехугольник ABCD — параллелограмм. Для параллелограмма известно, что отрезок, соединяющий середины противоположных сторон, равен полусумме этих сторон. Следовательно:
\( MN = \frac{AB + BC}{2}. \)
Это равенство выполняется всегда, независимо от расположения сторон.
Таким образом, если выполняется условие \( MN = \frac{AB + BC}{2} \), то четырехугольник ABCD либо является параллелограммом, либо равнобедренной трапецией.
Ответ: ABCD — параллелограмм или равнобедренная трапеция.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!