ГДЗ по Геометрии 9 класс Номер 859 Атанасян — Подробные Ответы

Докажите, что если сумма расстояний между серединами противоположных сторон выпуклого четырёхугольника равна половине его периметра, то этот четырёхугольник — параллелограмм. 

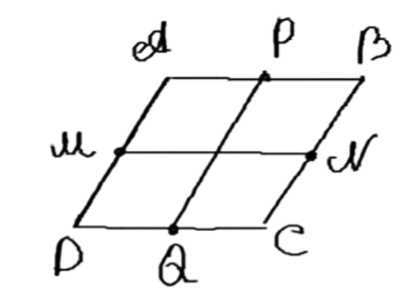
Дано: ABCD — выпуклый четырехугольник, точки \( M, N, P, Q \) — середины сторон \( AB, BC, CD, DA \) соответственно. Условие: \( MP + NQ = \frac{AB + BC + CD + AD}{2} \). Требуется доказать, что ABCD — параллелограмм.

Решение:
1. Пусть стороны ABCD попарно не параллельны.
Согласно ранее доказанным утверждениям (например, из задачи №858), выполняются следующие неравенства:
\( MP < \frac{AD + BC}{2}, \)
\( NQ < \frac{AB + CD}{2}. \)

Сложим эти два неравенства:
\( MP + NQ \leq \frac{AD + BC}{2} + \frac{AB + CD}{2} = \frac{AB + BC + CD + AD}{2}. \)

Это противоречит условию задачи, так как равенство не достигается, если стороны ABCD попарно не параллельны. Следовательно, этот случай невозможен.

2. Рассмотрим случай, когда \( AD \parallel BC \), но \( AB \) не параллельно \( CD \).
В этом случае:
\( MP < \frac{AD + BC}{2}, \)
\( NQ = \frac{AB + CD}{2}, \) так как \( NQ \) является средней линией трапеции с основаниями \( AB \) и \( CD \).

Сложим:
\( MP + NQ \leq \frac{AD + BC}{2} + \frac{AB + CD}{2} = \frac{AB + BC + CD + AD}{2}. \)

Равенство выполняется, но только в некоторых случаях, когда точки \( M \) и \( N \) совпадают с их теоретическими положениями. Однако это условие не гарантирует, что ABCD является параллелограммом.

3. Рассмотрим случай, когда \( AD \parallel BC \) и \( AB \parallel CD \).
В этом случае:
\( MP = \frac{AD + BC}{2}, \) так как \( MP \) является средней линией трапеции с основаниями \( AD \) и \( BC \),
\( NQ = \frac{AB + CD}{2}, \) так как \( NQ \) является средней линией трапеции с основаниями \( AB \) и \( CD \).

Сложим:
\( MP + NQ = \frac{AD + BC}{2} + \frac{AB + CD}{2} = \frac{AB + BC + CD + AD}{2}. \)

Равенство выполняется всегда, если стороны попарно параллельны. Следовательно, ABCD — параллелограмм.

Вывод: доказано, что если выполняется равенство \( MP + NQ = \frac{AB + BC + CD + AD}{2} \), то ABCD является параллелограммом.

Дано: ABCD — выпуклый четырехугольник, точки \( M, N, P, Q \) — середины сторон \( AB, BC, CD, DA \) соответственно. Условие: \( MP + NQ = \frac{AB + BC + CD + AD}{2} \). Требуется доказать, что ABCD — параллелограмм.

Решение:

1. Пусть стороны ABCD попарно не параллельны.
Согласно доказанному ранее (смотрите задачу №858), выполняются следующие неравенства:
\( MP < \frac{AD + BC}{2}, \)
\( NQ < \frac{AB + CD}{2}. \)

Сложим эти два неравенства:
\( MP + NQ \leq \frac{AD + BC}{2} + \frac{AB + CD}{2} = \frac{AB + BC + CD + AD}{2}. \)

Это противоречит условию задачи, так как равенство не достигается при условии, что стороны ABCD попарно не параллельны. Следовательно, этот случай невозможен.

2. Рассмотрим случай, когда \( AD \) параллельно \( BC \), но \( AB \) не параллельно \( CD \).
В этом случае:
\( MP < \frac{AD + BC}{2}, \)
\( NQ = \frac{AB + CD}{2}, \) так как \( NQ \) является средней линией трапеции с основаниями \( AB \) и \( CD \).

Сложим:
\( MP + NQ \leq \frac{AD + BC}{2} + \frac{AB + CD}{2} = \frac{AB + BC + CD + AD}{2}. \)

Равенство выполняется, но только в некоторых случаях, когда точки \( M \) и \( N \) совпадают со своими теоретическими положениями. Однако это условие не гарантирует, что ABCD является параллелограммом.

3. Рассмотрим последний случай, когда \( AD \) параллельно \( BC \) и \( AB \) параллельно \( CD \).
В этом случае:
\( MP = \frac{AD + BC}{2}, \) так как \( MP \) является средней линией трапеции с основаниями \( AD \) и \( BC \),
\( NQ = \frac{AB + CD}{2}, \) так как \( NQ \) является средней линией трапеции с основаниями \( AB \) и \( CD \).

Сложим:
\( MP + NQ = \frac{AD + BC}{2} + \frac{AB + CD}{2} = \frac{AB + BC + CD + AD}{2}. \)

Равенство выполняется всегда, если стороны попарно параллельны. Следовательно, ABCD — параллелограмм.

Вывод: доказано, что если выполняется равенство \( MP + NQ = \frac{AB + BC + CD + AD}{2} \), то ABCD является параллелограммом.