
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 857 Атанасян — Подробные Ответы
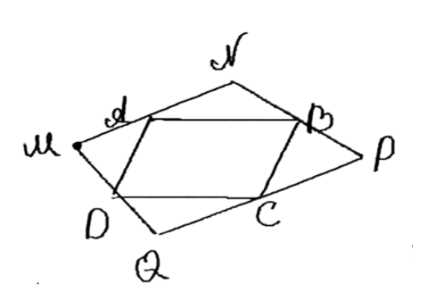
Точка \( M \) не лежит на прямых, содержащих стороны параллелограмма \( ABCD \). Докажите, что существуют точки \( N \), \( P \) и \( Q \), расположенные так, что \( A \), \( B \), \( C \) и \( D \) являются соответственно серединами отрезков \( MN \), \( NP \), \( PQ \) и \( QM \).
Дано: ABCD — параллелограмм.
Доказать: существует выпуклый четырехугольник MNPQ, вершины которого симметричны относительно точек A, B, C, D, являющихся серединами сторон.
Решение:
1. Построим точку M вне параллелограмма ABCD и не лежащую на прямых, содержащих его стороны.
Получаем:
— точка N симметрична M относительно точки A;
— точка P симметрична N относительно точки B;
— точка Q симметрична P относительно точки C.
2. Чтобы доказать, что D принадлежит MQ и MD = DQ, нужно показать, что точка M симметрична точке Q относительно точки D.
3. Рассмотрим треугольник QPN, в котором:
— BC, сторона параллелограмма, является средней линией;
— BC параллельна NQ.
Следовательно, в треугольнике QMN:
— AD параллельна BC и NQ;
— MA = AN.
4. Таким образом, AD является средней линией треугольника QMN, а MD = DQ.
Что и требовалось доказать.
Дано: ABCD — параллелограмм.
Необходимо доказать, что существует выпуклый четырехугольник MNPQ, вершины которого симметричны относительно точек A, B, C, D, являющихся серединами сторон параллелограмма.
Решение:
1. Построим точку \( M \), которая находится вне параллелограмма \( ABCD \) и не лежит на прямых, содержащих стороны параллелограмма.
Определим симметричные точки:
— точка \( N \) симметрична \( M \) относительно точки \( A \);
— точка \( P \) симметрична \( N \) относительно точки \( B \);
— точка \( Q \) симметрична \( P \) относительно точки \( C \).
2. Чтобы доказать утверждение, необходимо показать, что точка \( D \) принадлежит прямой \( MQ \), а также \( MD = DQ \). Это эквивалентно утверждению, что точка \( M \) симметрична точке \( Q \) относительно точки \( D \).
3. Рассмотрим треугольник \( QPN \).
В этом треугольнике сторона \( BC \) параллелограмма является средней линией.
Средняя линия \( BC \) параллельна прямой \( NQ \), так как стороны параллелограмма \( AB \parallel CD \) и \( AD \parallel BC \).
Следовательно, в треугольнике \( QMN \):
— \( AD \parallel BC \) и \( AD \parallel NQ \) (по свойствам параллелограмма);
— \( MA = AN \), так как точка \( N \) симметрична \( M \) относительно точки \( A \).
4. Поскольку \( AD \) является средней линией треугольника \( QMN \), то точка \( D \) делит отрезок \( MQ \) пополам, то есть \( MD = DQ \).
Таким образом, доказано, что точка \( M \) симметрична точке \( Q \) относительно точки \( D \), а точка \( D \) принадлежит прямой \( MQ \).
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!