ГДЗ по Геометрии 9 класс Номер 856 Атанасян — Подробные Ответы

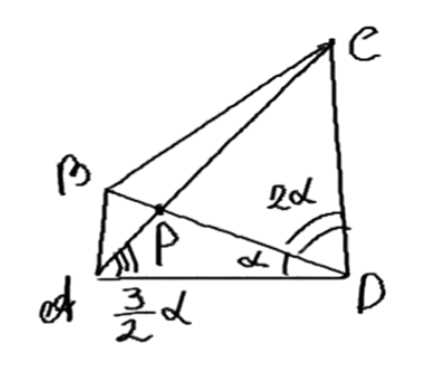
Диагонали выпуклого четырёхугольника \( ABCD \) пересекаются в точке \( P \). Известно, что \( \angle ADP = \frac{1}{2} \angle PDC \), \( \angle ADP = \frac{2}{3} \angle PAD \) и \( AD = BD = CD \).  

а) Найдите все углы четырёхугольника.  

б) Докажите, что \( AB^2 = BP \cdot BD \).

Рассмотрим краткое решение задачи.

Дано: \( ABCD \) — выпуклый четырехугольник, \( P = AC \cap BD \), \( \angle ADP = \frac{1}{2} \angle PDC \), \( \angle ADP = \frac{1}{2} \angle PAD \), \( AD = BD = CD \).
Найти: \( \angle A \), \( \angle B \), \( \angle C \), \( \angle D \).
Доказать: \( AB^2 = BP \cdot BD \).

Решение:

1. Обозначим \( \angle ADP = \alpha \), тогда \( \angle PDC = 2\alpha \), \( \angle PAD = \frac{3}{2}\alpha \).
2. \( AD = BD = CD \), значит, точки \( A, B, C \) лежат на окружности радиуса \( AD \).
3. На дуге \( AB \), вписанный угол \( \angle LACB = \frac{\alpha}{2} \).
4. На дуге \( BC \), вписанный угол \( \angle LBAC = \alpha \).
5. Углы четырехугольника:
— \( \angle A = \angle 2BAC + \angle PAD = \frac{3}{2}\alpha + 2\alpha = \frac{5}{2}\alpha \),
— \( \angle D = \alpha + 2\alpha = 3\alpha \),
— \( \angle C = \angle LACB + \angle LACD = \frac{\alpha}{2} + \frac{3}{2}\alpha = 2\alpha \),
— \( \angle B = \angle A + \angle C = \frac{5}{2}\alpha + 2\alpha = \frac{9}{2}\alpha \).

6. Сумма углов четырехугольника:
\[
\frac{5}{2}\alpha + \frac{9}{2}\alpha + 2\alpha + 3\alpha = 360^\circ.
\]
\[
12\alpha = 360^\circ, \quad \alpha = 30^\circ.
\]

7. Получаем:
\[
\angle A = \frac{5}{2} \cdot 30^\circ = 75^\circ, \quad \angle B = \frac{9}{2} \cdot 30^\circ = 135^\circ, \quad \angle C = 2 \cdot 30^\circ = 60^\circ, \quad \angle D = 3 \cdot 30^\circ = 90^\circ.
\]

Доказательство:
Рассмотрим треугольники \( \triangle ABP \) и \( \triangle DBA \):
Угол \( \angle B \) общий, \( \angle BAP = \angle BDA = \alpha = 30^\circ \).
Отсюда получаем, что по двум углам \( \triangle ABP \sim \triangle DBA \), значит:
\[
\frac{AB}{BD} = \frac{BP}{AB}.
\]
Следовательно:
\[
AB^2 = BP \cdot BD.
\]
Что и требовалось доказать.

Дано: ABCD — выпуклый четырехугольник, P = AC ∩ BD, ∠ADP = ½∠PDC, ∠ADP = ½∠PAD, AD = BD = CD.
Найти: ∠A, ∠B, ∠C, ∠D.
Доказать: AB² = BP · BD.

Решение:

1. Обозначим ∠ADP = α. Тогда по условию ∠PDC = 2α, а также ∠PAD = 3/2 α.
2. Поскольку AD = BD = CD, точки A, B, C лежат на окружности радиуса AD.
3. Рассмотрим дугу AB. Вписанный угол ∠LACB опирается на эту дугу, следовательно, его величина равна половине величины дуги:
∠LACB = α/2.
4. Рассмотрим дугу BC. Вписанный угол ∠LBAC опирается на эту дугу, следовательно, его величина равна половине величины дуги:
∠LBAC = α.
5. Найдем углы четырехугольника:
∠A = ∠LBAC + ∠PAD = α + 3/2 α = 5/2 α.
∠D = ∠ADP + ∠PDC = α + 2α = 3α.
∠C = ∠LACB + ∠LACD = α/2 + 3/2 α = 2α.
∠B = ∠A + ∠C = 5/2 α + 2α = 9/2 α.

6. Сумма углов четырехугольника:
5/2 α + 9/2 α + 2α + 3α = 360°.
Приведем подобные члены:
12α = 360°.
Найдем α:
α = 360° / 12 = 30°.

7. Подставим значение α в найденные углы:
∠A = 5/2 · 30° = 75°.
∠B = 9/2 · 30° = 135°.
∠C = 2 · 30° = 60°.
∠D = 3 · 30° = 90°.

Ответ: ∠A = 75°, ∠B = 135°, ∠C = 60°, ∠D = 90°.

Доказательство:
Рассмотрим треугольники ABP и DBA.
Угол ∠B общий. Также ∠BAP = ∠BDA = α = 30°.
По признаку подобия треугольников (два угла), треугольники ABP и DBA подобны.
Из подобия следует:
AB / BD = BP / AB.
Умножим обе стороны на AB:
AB² = BP · BD.

Что и требовалось доказать.